2022-2023學年山西省朔州市應縣八年級（下）期末數學試卷

一、選擇題（本大題有10個小題，每小題3分，共30分。在每小題給出的四個選項中，只有一項符合題目要求，請將正確答案的字母標號填入下表相應的空格內。）

• 1．9的平方根是（　　）

  A．±3

  B．3

  C．-3

  D．± 3
  組卷：632引用：29難度：0.9

  解析

• 2．下列計算正確的是（　　）

  A． 3 + 2 = 5

  B． 3 × 2 = 6

  C． 3 - 2 = 1

  D． 18 ÷ 3 = 6
  組卷：313引用：7難度：0.6

  解析

• 3．一次函數y=-2x+4的圖象與y軸交點的坐標是（　　）

  A．（2，0）

  B．（0，4）

  C．（4，0）

  D． （ 0 ， 1 2 ）
  組卷：756引用：4難度：0.8

  解析

• 4．對于函數y=4x,下列說法正確的是（　　）

  A．當x＞0時，y隨x的增大而減小

  B．當x＜0時，y隨x的增大而減小

  C．y隨x的增大而減小

  D．y隨x的增大而增大
  組卷：784引用：3難度：0.7

  解析

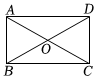• 5．如圖，四邊形ABCD為矩形，對角線AC與BD交于點O，以下說法不一定正確的是（　　）

  A．∠BAD=90°

  B．AC=BD

  C．∠BAC=∠DAC

  D．AO=OC
  組卷：172引用：2難度：0.7

  解析

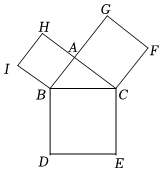• 6．如圖，Rt△ABC中，∠BAC=90°，分別以邊AB，CA，BC向外作正方形，正方形ABIH的面積為25，正方形BDEC的面積為169，則正方形ACFG的面積是（　　）

  A．194

  B．144

  C．122

  D．110
  組卷：1336引用：4難度：0.5

  解析

• 7．學校準備從甲、乙、丙、丁四個科創小組中選出一組代表學校參加青少年科技創新大賽，各組的平時成績的平均數（單位：分）及方差如表所示：如果要選出一個成績較好且狀態穩定的組去參賽，那么應選的組是（　　）

  	甲	乙	丙	丁
  平均數	7	8	8	7
  方差	1	1	1.2	1.8

  A．甲

  B．乙

  C．丙

  D．丁
  組卷：98引用：5難度：0.7

  解析

三、解答題（共75分，解答應寫出文字說明，證明過程或演算步驟）

• 22．勾股定理是人類最偉大的十個科學發現之一，西方國家稱之為畢達哥拉斯定理．在我國古書《周髀算經》中就有“若勾三，股四，則弦五”的記載，我國漢代數學家趙爽為了證明勾股定理，創制了一幅“弦圖”（如圖1），后人稱之為“趙爽弦圖”，流傳至今．
  
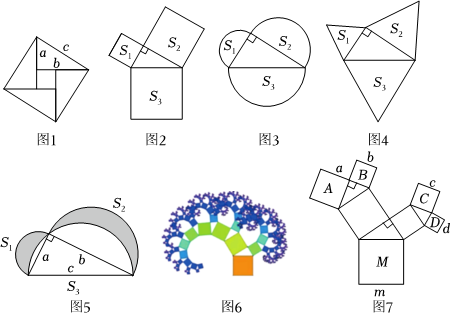
  （1）①如圖2，3，4，以直角三角形的三邊為邊或直徑，分別向外部作正方形、半圓、等邊三角形，面積分別為S₁，S₂，S₃，利用勾股定理，判斷這3個圖形中面積關系滿足S₁+S₂=S₃的有

  個．
  ②如圖5，分別以直角三角形三邊為直徑作半圓，設圖中兩個月牙形圖案（圖中陰影部分）的面積分別為S₁，S₂，直角三角形面積為S₃，也滿足S₁+S₂=S₃嗎？若滿足，請證明；若不滿足，請求出S₁，S₂，S₃的數量關系．
  （2）如果以正方形一邊為斜邊向外作直角三角形，再以該直角三角形的兩直角邊分別向外作正方形，重復這一過程就可以得到如圖6所示的“勾股樹”．在如圖7所示的“勾股樹”的某部分圖形中，設大正方形M的邊長為定值m,四個小正方形A，B，C，D的邊長分別為a,b,c,d,則a²+b²+c²+d²=

  ．
  組卷：664引用：4難度：0.6

  解析

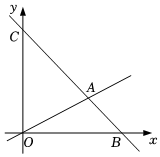• 23．如圖，在平面直角坐標系中，過點C（0，6）的直線AB與直線OA相交于點A（4，2），動點M在直線OA和射線AC上運動．
  （1）求直線AB的解析式；
  （2）求△OAB的面積；
  （3）是否存在點M，使△OMC的面積是△OAB的面積的

  1

  2

  ？若存在，求出此時點M的坐標；若不存在，說明理由．
  組卷：728引用：4難度：0.3

  解析