2022年山東省日照二中中考數學二模試卷

一、選擇題（共12小題，每小題3分，滿分36分）

• 1．袁隆平院士被譽為“雜交水稻之父”，經過他帶領的團隊多年艱苦努力，目前我國雜交水稻種植面積達2.4億畝，每年增產的糧食可以養活8000萬人，將數據8000萬用科學記數法表示為8×10ⁿ，則n的值為（　　）

  A．7

  B．8

  C．9

  D．10
  組卷：110引用：4難度：0.8

  解析

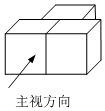• 2．三個大小一樣的正方體按如圖方式擺放，它的主視圖是（　　）

  A．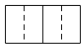

  B．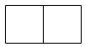

  C．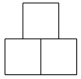

  D．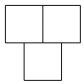
  組卷：156引用：3難度：0.8

  解析

• 3．手機已逐漸成為人們日常通訊的主要工具，其背后離不開通訊運營商的市場支持，如圖展現的是我國四大通訊運營商的企業圖標，其中是軸對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：191引用：15難度：0.8

  解析

• 4．設6-

  10

  的整數部分為a,小數部分為b,則（2a+

  10

  ）b的值是（　　）

  A．6

  B．2 10

  C．12

  D．9 10
  組卷：5017引用：35難度：0.8

  解析

• 5．定義新運算：a※b=

  a - 1 （ a ≤ b ）

  - a b （ a ＞ b 且 b ≠ 0 ）

  ，則函數y=3※x的圖象大致是（　　）

  A．

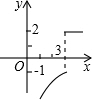
  B．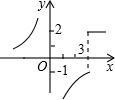

  C．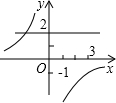

  D．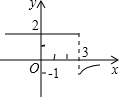
  組卷：1120引用：29難度：0.9

  解析

• 6．若x₁，x₂是x²+bx-3b=0的兩個根，且x₁²+x₂²=7，則b的值是（　　）

  A．-7

  B．1

  C．1或7

  D．7或-1
  組卷：1728引用：4難度：0.5

  解析

• 7．若關于x的不等式組

  x + 1 ＜ 3 x + 1 2

  4 x - 1 ≥ 3 （ a - x ）

  的解集是x＞1，關于y的分式方程

  a

  y

  -

  1

  =

  5

  y

  -

  8

  y

  -

  1

  -

  2

  的解為非負數，則所有符合條件的整數a的和為（　　）

  A．-18

  B．-15

  C．0

  D．2
  組卷：159引用：3難度：0.6

  解析

三、解答題（共68分）

• 21．【問題提出】
  （1）如圖1，在矩形ABCD中，AD=10，AB=12，點E為AD的中點，點P為矩形ABCD內以BC為直徑的半圓上一點，則PE的最小值為

  ；
  【問題探究】
  （2）如圖2，在△ABC中，AD為BC邊上的高，且AD=BC=4，點P為△ABC內一點，當

  S

  △

  PBC

  =

  1

  2

  S

  △

  ABC

  時，求PB+PC的最小值；
  【問題解決】
  （3）李伯伯家有一塊直角三角形菜園ABC，如圖3，

  BC

  =

  200

  3

  米，∠C=90°，∠ABC=60°，李伯伯準備在該三角形菜園內取一點P，使得∠APB=120°，并在△ABP內種植當季蔬菜，邊BC的中點D為菜園出入口，為了種植方便，李伯伯打算在AC邊上取點E，并沿PE、DE修兩條人行走道，為了節省時間，要求人行走道的總長度（PE+DE）盡可能小，問PE+DE的長度是否存在最小值？若存在，求出其最小值；若不存在，請說明理由．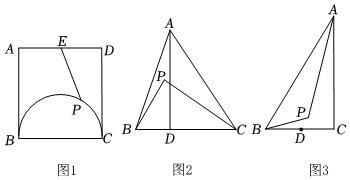
  
  組卷：365引用：4難度：0.3

  解析

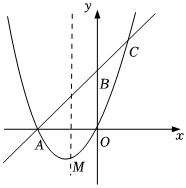• 22．在平面直角坐標系中，拋物線y=

  1

  2

  x²+bx+c經過點A（-4，0），點M為拋物線的頂點，點B在y軸上，直線AB與拋物線在第一象限交于點C（2，6），如圖
  （1）求拋物線的解析式；
  （2）連接OC，若過點O的直線交線段AC于點P，將△MOC的面積分成1：2的兩部分，求點P的坐標；
  （3）若Q是直線AC上方拋物線上一個動點（不與點A、C重合），當△QAC的面積等于△AOC的面積時，求出Q點坐標．
  （4）在拋物線的對稱軸上有一動點H，在拋物線上是否存在一點N，使以點A、H、C、N為頂點的四邊形是平行四邊形？若存在，求出點N的坐標；若不存在，請說明理由．
  組卷：245引用：3難度：0.1

  解析