2022-2023學年上海市松江一中高一（下）段考數學試卷

一、填空題（1-6每題4分，7-12每題5分，共54分）

• 1．角2023°是第象限角

  ．
  組卷：292引用：6難度：0.9

  解析

• 2．半徑為2的扇形面積為4π，則扇形所對圓心角的弧度數為

  ．
  組卷：23引用：2難度：0.7

  解析

• 3．已知角α的終邊經過點P（4，-3），則sinα+cosα=

   

  ．
  組卷：38引用：3難度：0.9

  解析

• 4．已知cos（

  3

  π

  8

  -α）=

  1

  3

  ，則cos（

  5

  π

  8

  +α）=

  ．
  組卷：72引用：2難度：0.7

  解析

• 5．若

  x

  ∈

  （

  π

  2

  ，

  π

  ）

  ，

  sinx

  =

  2

  3

  ，則x=

  ．（用符號arcsin表示）
  組卷：16引用：2難度：0.8

  解析

• 6．若θ為銳角，則

  lo

  g

  sinθ

  （

  1

  +

  cot

  2

  θ

  ）

  =

  ．
  組卷：69引用：3難度：0.8

  解析

• 7．若

  0

  ＜

  α

  ＜

  π

  2

  ，-

  π

  2

  ＜

  β

  ＜

  0

  ，

  cos

  （

  π

  4

  +

  α

  ）

  =

  1

  3

  ，

  cos

  （

  π

  4

  -

  β

  2

  ）

  =

  3

  3

  ，則

  cos

  （

  α

  +

  β

  2

  ）

  =

  ．
  組卷：533引用：16難度：0.5

  解析

三、解答題

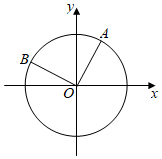• 20．閱讀問題：已知點A（

  1

  2

  ，

  3

  2

  ），將OA繞坐標原點逆時針旋轉

  π

  2

  至OB，求點B的坐標
  解：如圖，點A在角α的終邊上，且OA=1，則cosα=

  1

  2

  ，sinα=

  3

  2

  ，點B在角α+
  

  π

  2

  的終邊上，且OB=1，于是點B的坐標滿足：
  x_B=cos（

  α

  +

  π

  2

  ）=-sinα=-

  3

  2

  ，y_B=sin（

  α

  +

  π

  2

  ）=cosα=

  1

  2

  ，即B（-

  3

  2

  ，

  1

  2

  ）．
  （1）將OA繞原點順時針旋轉

  π

  2

  并延長至點C使OC=4OA，求點C坐標；
  （2）若將OA繞坐標原點旋轉θ并延長至ON，使ON=r?OA（r＞0），求點N的坐標．（用含有r、θ的數學式子表示）
  （3）定義P（x₁，y₁），Q（x₂，y₂）的中點為（

  x

  1

  +

  x

  2

  2

  ，

  y

  1

  +

  y

  2

  2

  ），將OA逆時針旋轉β角，并延長至OD，使OD=2?OA，且DA的中點M也在單位圓上，求cosβ的值．
  組卷：49引用：2難度：0.6

  解析

• 21．在非直角三角形ABC中，角A，B，C的對邊分別為a,b,c,
  （1）若a+c=2b,求角B的最大值；
  （2）若a+c=mb（m＞1），
  （i）證明：

  tan

  A

  2

  tan

  C

  2

  =

  m

  -

  1

  m

  +

  1

  ；
  （可能運用的公式有

  sinα

  +

  sinβ

  =

  2

  sin

  α

  +

  β

  2

  cos

  α

  -

  β

  2

  ）
  （ii）是否存在函數φ（m），使得對于一切滿足條件的m,代數式

  cos

  A

  +

  cos

  C

  +

  φ

  （

  m

  ）

  φ

  （

  m

  ）

  cos

  A

  cos

  C

  恒為定值？若存在，請給出一個滿足條件的φ（m），并證明之；若不存在，請給出一個理由．
  組卷：378引用：5難度：0.5

  解析