2022-2023學年浙江省寧波市慈溪市高二（上）期末數學試卷

一、選擇題（本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．直線x-2y+2=0在x軸上的截距是（　　）

  A．1

  B．-1

  C．-2

  D．2
  組卷：236引用：3難度：0.8

  解析

• 2．雙曲線

  y

  2

  -

  x

  2

  3

  =

  1

  的一個焦點的坐標為（　　）

  A．（0，2）

  B．（2，0）

  C．（0， 2 ）

  D． （ 2 ，0）
  組卷：143引用：1難度：0.9

  解析

• 3．某汽車集團公司大力發展新能源汽車，已知2021年全年生產新能源汽車4500輛．如果在后續的幾年中，后一年新能源汽車的產量是前一年的160%，那么2030年全年生產新能源汽車（　　）

  A．4500×1.67輛	B．4500×1.68輛
  C．4500×1.69輛	D．4500×1.610輛
  組卷：22引用：1難度：0.7

  解析

• 4．在空間直角坐標系Oxyz中，點（1，-2，5）關于z軸的對稱點的坐標為（　　）

  A．（1，2，-5）

  B．（-1，-2，-5）

  C．（-1，2，5）

  D．（-1，2，-5）
  組卷：44引用：3難度：0.7

  解析

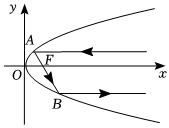• 5．如圖，某種探照燈的軸截面是拋物線y²=x（焦點F），平行于對稱軸的一光線，經射入點A反射過F到點B，再經反射，平行于對稱軸射出光線，則入射點A到反射點B的光線距離|AB|最短時點A的坐標是（　　）

  A．（ 1 4 ， 1 2 ）

  B．（ 1 2 ， 2 2 ）

  C．（1，1）

  D．（2， 2 ）
  組卷：59引用：1難度：0.7

  解析

• 6．若直線y=kx+2-3k與圓x²+y²+4y-57=0相交于不同兩點A，B，則弦AB長的最小值為（　　）

  A．10

  B．12

  C．14

  D．16
  組卷：114引用：2難度：0.7

  解析

• 7．已知數列{a_n}滿足：a₁=2，a_n+1=a_n（a_n-1）+1，給出兩個結論：①a₂₀₂₃=1+a₁a₂a₃…a₂₀₂₂；②

  1

  a

  1

  +

  1

  a

  2

  +

  1

  a

  3

  +

  …

  +

  1

  a

  2013

  ＞1，則（　　）

  A．①成立，②成立	B．①成立，②不成立
  C．①不成立，②成立	D．①不成立，②不成立
  組卷：122引用：1難度：0.5

  解析

四、解答題（本題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟

• 21．為了促銷，某大型電器商場，對某種型號的進口電視機銷售進行分期付款，規定：現場購買時先付款

  1

  4

  ，其余的

  3

  4

  在2年（24個月，不得提前）內每月（首付日后的第30天）固定支付等額數量的錢（設A元），以一月為一期計算復利．已知此電視機每臺售價為24000元，月息0.45%．[溫馨提示：分期付款公平交易原則：余款和分期付款的已付款均有利息收入．]
  （1）若有本金18000元，月息0.45%，復利計，求經過24個月后的本息和；（精確到1元）
  （2）求A的值．（精確到1元）
  （可用參考數據：1.0045²²=1.104，1.0045²³=1.109，1.0045²⁴=1.114，1.0045²⁵=1.119．）
  組卷：38引用：1難度：0.6

  解析

• 22．已知橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的離心率為

  2

  2

  ，且四個頂點構成的四邊形面積等于8

  2

  ．
  （1）求橢圓C的方程；
  （2）設橢圓C的左焦點為F，若直線l過定點（0，1）且與橢圓C相交于A，B兩點，求|FA|+|FB|的最大值．
  組卷：138引用：1難度：0.6

  解析