2023年海南省瓊中縣中考數學一模試卷

一、選擇題（本大題共12小題，每小題3分，共36分.在每小題給出的四個選項中，只有一個選項是符合題目要求的）

• 1．若非零數a,b互為相反數，下列四組數中，互為相反數的個數為（　　）
  ①a²與b²；②a²與-b²；③a³與b³；④a³與-b³．

  A．0

  B．1

  C．2

  D．3
  組卷：826引用：12難度：0.6

  解析

• 2．在一項科學研究中，科學家對人體血液中尺寸小于0.000508毫米的微小顆粒進行分析，發現在部分血液樣本中含有“微塑料”顆粒，這是科學家首次在人類血液中檢測到“微塑料”污染．我們可以把數據“0.000508”用科學記數法表示為（　　）

  A．5.08×10-5

  B．5.08×10-4

  C．50.8×10-5

  D．508×10-6
  組卷：145引用：3難度：0.8

  解析

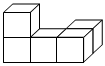• 3．如圖中幾何體從正面看能得到（　　）

  A．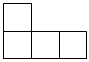

  B．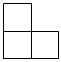

  C．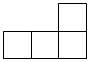

  D．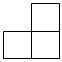
  組卷：145引用：11難度：0.9

  解析

• 4．將不等式x-3≥0的解集表示在數軸上，正確的是（　　）

  A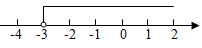．	B．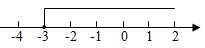
  C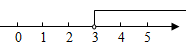．	D．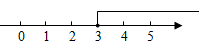
  組卷：124引用：9難度：0.7

  解析

• 5．下列命題中，真命題是（　　）

  A．相等的角是對頂角

  B．在同一平面內，垂直于同一條直線的兩條直線平行

  C．兩條直線被第三條直線所截，同位角相等

  D．同旁內角互補
  組卷：627引用：14難度：0.6

  解析

• 6．某小組長統計組內5人一天在課堂上的發言次數分別為3，3，0，4，5．關于這組數據，下列說法錯誤的是（　　）

  A．眾數是3

  B．中位數是0

  C．平均數是3

  D．極差是5
  組卷：531引用：12難度：0.7

  解析

• 7．一個不透明的袋子中裝有2個紅球和若干個黃球，這些球除顏色外都相同．經過多次試驗發現，摸出紅球的頻率穩定在

  1

  3

  左右，則袋子中的黃球個數最有可能是（　　）

  A．1

  B．2

  C．4

  D．6
  組卷：582引用：12難度：0.6

  解析

三、（本大題共6小題，17題12分，18、19、20題各10分，21、22題15分，本大題滿分72分）

• 21．【問題呈現】阿基米德折弦定理：阿基米德（archimedes,公元前287-公元前212年，古希臘）是有史以來最偉大的數學家之一，他與牛頓、高斯并稱為三大數學王子．如圖1，AB和BC是⊙O的兩條弦（即折線ABC是圓的一條折弦），BC＞AB，點M是

  ?

  ABC

  的中點，則從M向BC所作垂線的垂足D是折弦ABC的中點，即CD=DB+BA．下面是運用“截長法”證明CD=DB+BA的部分證明過程．
  證明：如圖2，在CD上截取CG=AB，連接MA、MB、MC和MG．
  ∵M是

  ?

  ABC

  的中點，
  ∴MA=MC，
  又∵∠A=∠C，BA=GC，
  ∴△MAB≌△MCG，
  ∴MB=MG，
  又∵MD⊥BC，
  ∴BD=DG，
  ∴AB+BD=CG+DG即CD=DB+BA．
  【理解運用】如圖1，AB、BC是⊙O的兩條弦，AB=4，BC=6，點M是

  ?

  ABC

  的中點，MD⊥BC于點D，則BD=

  ；
  【變式探究】如圖3，若點M是

  ?

  AC

  的中點，【問題呈現】中的其他條件不變，判斷CD、DB、BA之間存在怎樣的數量關系？并加以證明．
  【實踐應用】如圖4，BC是⊙O的直徑，點A圓上一定點，點D圓上一動點，且滿足∠DAC=45°，若AB=6，⊙O的半徑為5，則AD=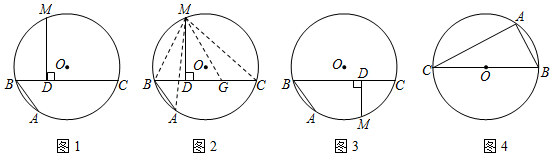

  ．
  
  組卷：1263引用：8難度：0.2

  解析

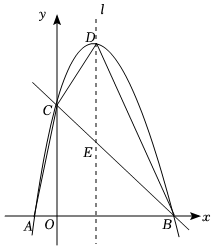• 22．如圖，拋物線y=ax²+3x+c（a≠0）與x軸交于點A（-2，0）和點B，與y軸交于點C（0，8），頂點為D，連接AC，CD，DB，直線BC與拋物線的對稱軸l交于點E．
  （1）求拋物線的解析式和直線BC的解析式；
  （2）求四邊形ABDC的面積；
  （3）P是第一象限內拋物線上的動點，連接PB，PC，當S_△PBC=

  3

  5

  S_△ABC時，求點P的坐標；
  （4）在拋物線的對稱軸l上是否存在點M，使得△BEM為等腰三角形？若存在，請直接寫出點M的坐標；若不存在，請說明理由．
  組卷：853引用：8難度：0.4

  解析