2021-2022學年河北省衡水市武強中學高二（下）期末數學試卷

一、單項選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．若集合M={x|

  x

  ＜4}，N={x|3x≥1}，則M∩N=（　　）

  A．{x|0≤x＜2}

  B．{x| 1 3 ≤x＜2}

  C．{x|3≤x＜16}

  D．{x| 1 3 ≤x＜16}
  組卷：5685引用：31難度：0.9

  解析

• 2．下列結論中正確的個數是（　　）
  ①命題“所有的四邊形都是矩形”是存在量詞命題；
  ②命題“?x∈R，x²+1＜0”是全稱量詞命題；
  ③命題“?x∈R，x²+2x+1≤0”的否定為“?x∈R，x²+2x+1≤0”；
  ④命題“a＞b是ac²＞bc²的必要條件”是真命題．

  A．0

  B．1

  C．2

  D．3
  組卷：1091引用：12難度：0.7

  解析

• 3．青少年視力是社會普遍關注的問題，視力情況可借助視力表測量．通常用五分記錄法和小數記錄法記錄視力數據，五分記錄法的數據L和小數記錄表的數據V的滿足L=5+lgV．已知某同學視力的五分記錄法的數據為4.9，則其視力的小數記錄法的數據為（　　）（

  10

  10

  ≈

  1

  .

  259

  ）

  A．1.5

  B．1.2

  C．0.8

  D．0.6
  組卷：247引用：18難度：0.6

  解析

• 4．設函數f（x）=

  1

  -

  x

  1

  +

  x

  ，則下列函數中為奇函數的是（　　）

  A．f（x-1）-1

  B．f（x-1）+1

  C．f（x+1）-1

  D．f（x+1）+1
  組卷：7560引用：37難度：0.6

  解析

• 5．已知x＞0，y＞0，2x+y=3，則9^x+3^y的最小值為（　　）

  A．27

  B．12 3

  C．12

  D．6 3
  組卷：369引用：2難度：0.8

  解析

• 6．函數y=（3^x-3^-x）cosx在區間[-

  π

  2

  ，

  π

  2

  ]的圖像大致為（　　）

  A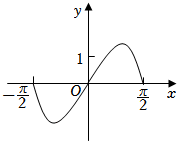．	B．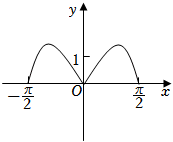
  C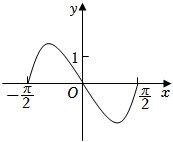．	D．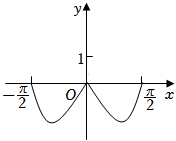
  組卷：2578引用：15難度：0.6

  解析

• 7．已知a=log₅2，b=log₈3，c=

  1

  2

  ，則下列判斷正確的是（　　）

  A．c＜b＜a

  B．b＜a＜c

  C．a＜c＜b

  D．a＜b＜c
  組卷：6195引用：34難度：0.7

  解析

四．解答題：本題共6小題，17題10分，其余每題12分，共70分.

• 21．已知函數

  f

  （

  x

  ）

  =

  lo

  g

  1

  2

  1

  -

  kx

  x

  -

  1

  為奇函數．
  （I）求常數k的值；
  （Ⅱ）若a＞b＞1，試比較f（a）與f（b）的大小；
  （Ⅲ）若函數

  g

  （

  x

  ）

  =

  f

  （

  x

  ）

  -

  （

  1

  2

  ）

  x

  +

  m

  ，且g（x）在區間[3，4]上沒有零點，求實數m的取值范圍．
  組卷：571引用：6難度：0.1

  解析

• 22．已知f（x）=

  2

  x

  +

  λ

  2

  x

  +

  1

  為奇函數．
  （1）求λ的值；
  （2）若g（x）=f（2x-1）+1，n∈N^*，求

  g

  （

  0

  n

  ）

  +

  g

  （

  1

  n

  ）

  +

  g

  （

  2

  n

  ）

  +

  …

  +

  g

  （

  n

  n

  ）

  的值；
  （3）當n∈N^*時，h（n）=

  1

  f

  （

  n

  ）

  ，求證：h（1）+h（2）+…+h（n）≤n+

  7

  2

  -

  3

  2

  n

  ．
  組卷：21引用：2難度：0.3

  解析