2022-2023學年北京八中高二（上）期末數學試卷

一、選擇題共10小題，每小題4分，共40分。在每小題列出的四個選項中，選出符合題目要求的一項。

• 1．已知直線l₁：ax-y-1=0，l₂：ax+（a+2）y+1=0．若l₁⊥l₂，則實數a=（　　）

  A．-1或1

  B．0或1

  C．-1或2

  D．-3或2
  組卷：905引用：10難度：0.8

  解析

• 2．在

  （

  3

  x

  -

  2

  x

  ）

  8

  的展開式中，常數項為（　　）

  A．-112

  B．112

  C．-1120

  D．1120
  組卷：475引用：2難度：0.8

  解析

• 3．已知雙曲線C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （a＞0，b＞0）的離心率為

  5

  2

  ，則C的漸近線方程為（　　）

  A． y =± 1 4 x

  B． y =± 1 3 x

  C． y =± 1 2 x

  D．y=±x
  組卷：720引用：13難度：0.7

  解析

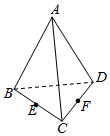• 4．如圖，在空間四邊形ABCD中，設E，F分別是BC，CD的中點，則

  AD

  +

  1

  2

  （

  BC

  -

  BD

  ）等于（　　）

  A． AD

  B． FA

  C． AF

  D． EF
  組卷：976引用：7難度：0.7

  解析

• 5．下列利用方向向量、法向量判斷線、面位置關系的結論中，正確的是（　　）

  A．兩條不重合直線l1，l2的方向向量分別是 a = （ 2 ，3，-1）， b = （ - 2 ，-3，1），則l1∥l2

  B．直線l的方向向量 a = （ 1 ，-1，2），平面α的法向量是 u = （ 6 ，4，-1），則l⊥α

  C．兩個不同的平面α，β的法向量分別是 u = （ 2 ，2，-1）， v = （ - 3 ，4，2），則α⊥β

  D．直線l的方向向量 a = （ 0 ，3，0），平面α的法向量是 u = （ 0 ，-5，0），則l∥α
  組卷：884引用：56難度：0.9

  解析

• 6．“a＞1”是“直線y=ax-1的傾斜角大于

  π

  4

  ”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：73引用：1難度：0.7

  解析

• 7．當動點P在正方體ABCD-A₁B₁C₁D₁的體對角線A₁C上運動時，異面直線BP與AD₁所成角的取值范圍是（　　）

  A．[ π 6 ， π 4 ]

  B．[ π 6 ， π 3 ]

  C．[ π 4 ， π 3 ]

  D．[ π 3 ， π 2 ]
  組卷：385引用：3難度：0.6

  解析

三、解答題共6小題，共85分，解答應寫出文字說明，演算步驟或證明過程。

• 20．已知橢圓C的中心在原點，焦點在x軸上，短軸長為

  2

  2

  ，離心率為

  3

  3

  ．
  （Ⅰ）求橢圓C的方程；
  （Ⅱ）一條動直線l與橢圓C交于不同兩點M，N，O為坐標原點，△OMN的面積為

  6

  2

  ，求證：|OM|²+|ON|²為定值．
  組卷：476引用：1難度：0.5

  解析

• 21．在平面直角坐標系中，O為坐標原點．對任意的點P（x,y），定義|OP|=|x|+|y|．任取點A（x₁，y₁），B（x₂，y₂），記A'（x₁，y₂），B'（x₂，y₁），若此時|OA|²+|OB|²≥|OA'|²+|OB'|²成立，則稱點A，B相關．
  （Ⅰ）分別判斷下面各組中兩點是否相關，并說明理由；
  ①A（-2，1），B（3，2）；②C（4，-3），D（2，4）．
  （Ⅱ）給定n∈N*，n≥3，點集Ω_n={（x,y）|-n≤x≤n,-n≤y≤n,x,y∈Z}．
  （i）求集合Ω_n中與點A（1，1）相關的點的個數；
  （ii）若S?Ω_n，且對于任意的A，B∈S，點A，B相關，求S中元素個數的最大值．
  組卷：271引用：14難度：0.6

  解析