2022-2023學年四川省成都市錦江區師一學校九年級（上）月考數學試卷（10月份）

一.選擇題（32）

• 1．下列方程是一元二次方程的是（　　）

  A．x2=2x+3

  B．x2+1=2xy

  C．x2+ 1 x =3

  D．2x+y=1
  組卷：884引用：10難度：0.7

  解析

• 2．若a、b、c、d是成比例線段，其中a=5cm,b=2.5cm,c=10cm,則線段d的長為（　　）

  A．2cm

  B．4cm

  C．5cm

  D．6cm
  組卷：2036引用：21難度：0.9

  解析

• 3．已知

  x

  y

  =

  2

  3

  ，則下列結論一定正確的是（　　）

  A．x=2，y=3

  B．2x=3y

  C． x x + y = 3 5

  D． x + y y = 5 3
  組卷：1326引用：12難度：0.7

  解析

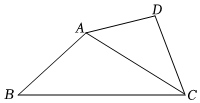• 4．如圖，已知：△ABC∽△DAC，∠B=37°，∠D=116°，∠BAD的度數為（　　）

  A．37°

  B．116°

  C．153°

  D．143°
  組卷：454引用：3難度：0.7

  解析

• 5．如圖，△ABC中，點D是AB上一點，補充下列條件后，仍不能判定△ADC∽△ACB的是（　　）

  A．∠ADC=∠ACB

  B．∠ACD=∠ABC

  C． AD AC = AC AB

  D． CD BC = AC AB
  組卷：767引用：8難度：0.5

  解析

• 6．下列命題是假命題的是（　　）

  A．有一組鄰邊相等的矩形是正方形

  B．對角線互相垂直的平行四邊形是正方形

  C．對角線相等的平行四邊形是矩形

  D．有三個角是直角的四邊形是矩形
  組卷：762引用：6難度：0.6

  解析

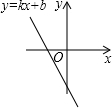• 7．已知函數y=kx+b的圖象如圖所示，則一元二次方程bx²+x+2-k=0的根的情況是（　　）

  A．有兩個不相等的實數根	B．沒有實數根
  C．有兩個相等的實數根	D．無法確定
  組卷：171引用：1難度：0.6

  解析

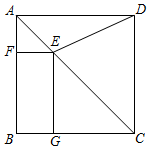• 8．如圖，在正方形ABCD中，點E在對角線AC上，EF⊥AB于點F，EG⊥BC于點G，連接DE，若AB=10，AE=3

  2

  ，則ED的長度為（　　）

  A．7

  B．2 10

  C． 58

  D． 82
  組卷：1484引用：8難度：0.6

  解析

五.解答題（30）

• 25．如圖，在菱形ABCD中，過點D作DE⊥AB于點E，菱形的對角線AC交DE于點F，連接BF．已知AB=5，DE=4．
  （1）求證：∠ABF=∠ADE；
  （2）連接CE交BF于點G，求

  BG

  BF

  的值；
  （3）已知點P為折線A-B-C上一動點，連接PF．當線段PB的長為何值時，∠BPF與∠BCD互為余角，并求此時直線DP與直線AC所夾銳角的正切值．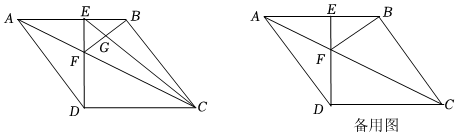
  組卷：708引用：3難度：0.1

  解析

• 26．【閱讀理解】
  定義：在同一平面內，有不在同一條直線上的三點M，N，P，連接PM，PN，設∠MPN=α，

  PM

  PN

  =k,則我們把（a,k）稱為點M到N關于點P的“度比坐標”，把（a,

  1

  k

  ）稱為點N到M關于點P的“度比坐標”．
  【遷移運用】
  如圖，直線l₁：y=x+5分別與x軸，y軸相交于A，B兩點，過點C（0，10）的直線l₂與l₁在第一象限內相交于點D．根據定義，我們知道點A到C關于點O的“度比坐標”為（90°，

  1

  2

  ）．
  （1）請分別直接寫出A，B兩點的坐標及點B到A關于點O的“度比坐標”；
  （2）若點A到C關于點D的“度比坐標”與點C到B關于點D的“度比坐標”相同．
  （ⅰ）求直線l₂的函數表達式；
  （ⅱ）點E，F分別是直線l₁，l₂上的動點，連接OE，OF，若點E到F關于點O的“度比坐標”為（90°，

  3

  5

  ），求此時點E的坐標．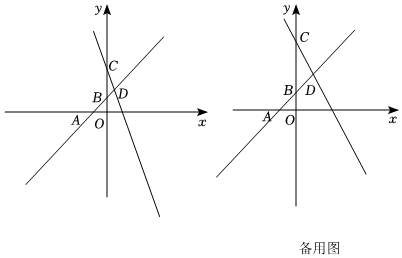
  
  組卷：979引用：3難度：0.1

  解析