2022-2023學年重慶市九龍坡區楊家坪中學八年級（上）期中數學試卷

一、選擇題（共12小題，每小題4分，滿分48分）

• 1．日常生活中，我們會看到很多標志，在以下綠色食品、回收、節能、節水四個標志中，是軸對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：699引用：36難度：0.9

  解析

• 2．下列各組數，可以作為三角形的三邊長的是（　　）

  A．1，3，4

  B．6，9，24

  C．9，13，21

  D．10，26，40
  組卷：134引用：5難度：0.6

  解析

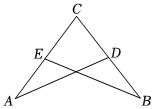• 3．如圖，已知△CAD≌△CBE，若∠A=30°，∠C=70°，則∠CEB=（　　）

  A．50°

  B．60°

  C．70°

  D．80°
  組卷：324引用：9難度：0.6

  解析

• 4．一個正六邊形的內角和的度數為（　　）

  A．1080°

  B．720°

  C．540°

  D．360°
  組卷：739引用：8難度：0.8

  解析

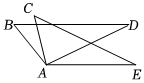• 5．如圖，已知AB=AC，AD=AE，欲證△ABD≌△ACE，不可補充的條件是（　　）

  A．BD=CE

  B．∠D=∠E

  C．∠BAD=∠CAE

  D．∠BAC=∠DAE
  組卷：264引用：5難度：0.7

  解析

• 6．在平面直角坐標系中，點P（6，-3）關于x軸對稱的點的坐標是（　　）

  A．（-6，3）

  B．（6，-3）

  C．（6，3）

  D．（-6，-3）
  組卷：112引用：2難度：0.9

  解析

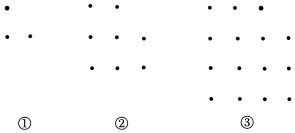• 7．如圖，把黑色小圓圈按照如圖所示的規律排列，其中第①個圖形中有3個黑色小圓圈，第②個圖形中有8個黑色小圓圈，第③個圖形中有15個黑色小圓圈，…，按照此規律，第⑩個圖形中黑色小圓圈的個數為（　　）

  A．63

  B．64

  C．99

  D．120
  組卷：67引用：1難度：0.7

  解析

• 8．小華在復習用尺規作一個角等于已知角的過程中，回顧了作圖的過程，他發現△OCD與△O′C′D′全等，請你說明小華得到全等的依據是（　　）
  

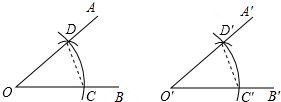
  A．SSS

  B．SAS

  C．ASA

  D．AAS
  組卷：483引用：13難度：0.5

  解析

四、解答題；（本大題7個小題，每小題10分，共70分）

• 24．[觀察發現]
  ①如圖1，△ABC中，AB=7，AC=5，點D為BC的中點，求AD的取值范圍．
  小明的解法如下：延長AD到點E，使DE=AD，連接CE，易證△ABD≌△ECD（SAS）可得AB=CE，在△AEC中根據三角形三邊關系可得2＜AE＜12，又∵AE=2AD，∴1＜AD＜6．
  ②如圖2，在△ABC中，若AB=AC，則∠B=∠C；若∠B=∠C，則AB=AC．
  [應用拓展]
  如圖3，∠BCA=60°，∠AED=120°，CB=CA，EA=ED，連接CD，F為CD的中點，連接FB、FE．求證：BF⊥EF．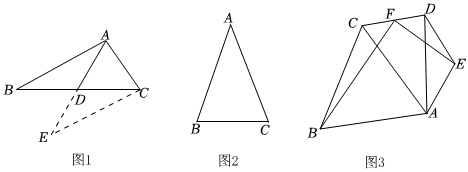
  
  組卷：109引用：2難度：0.3

  解析

• 25．（1）如圖1，在四邊形ABCD中，DA=DC，∠A=∠C=90°，E、F分別是邊AB、BC上的點，且∠EDF=

  1

  2

  ∠ADC，請直接寫出圖中線段AE、EF、FC之間的數量關系

  ．
  （2）如圖2，在四邊形ABCD中，DA=DC，∠A+∠C=180°，E、F分別是邊AB、BC上的點，且∠EDF=

  1

  2

  ∠ADC，上述結論是否仍然成立，并說明理由．
  （3）如圖3，在四邊形ABCD中，DA=DC，∠A+∠BCD=180°，E、F分別是邊AB、BC延長線上的點，且∠EDF=

  1

  2

  ∠ADC，（1）中的結論是否仍然成立？若成立，請證明；若不成立，線段AE、EF、FC之間又有怎樣的數量關系，請直接寫出你的猜想，并說明理由．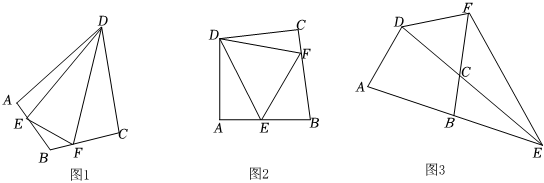
  
  組卷：165引用：1難度：0.2

  解析