當前位置：試卷中心 > 試卷詳情

2016-2017學年福建省泉州五中九年級（上）入學數學試卷

發布：2024/4/20 14:35:0

一、選擇題（共7小題，每小題3分，滿分21分）

1．已知點P（x,y）在函數y=
1
x
2
+
-
x
的圖象上，那么點P應在平面直角坐標系中的（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
組卷：810引用：51難度：0.9
解析
2．某班17名同學參加了數學競賽的預賽，預賽成績各不相同，現要從中選出9名同學參加決賽，小明已經知道了自己的成績，他想知道自己能否進入決賽，還需要知道這17名同學成績的（　　）
A．平均分 B．眾數 C．中位數 D．方差
組卷：269引用：5難度：0.9
解析
3．有甲、乙兩個箱子，其中甲箱內有98顆球，分別標記號碼1～98，且號碼為不重復的整數，乙箱內沒有球．已知小育從甲箱內拿出49顆球放入乙箱后，乙箱內球的號碼的中位數為40．若此時甲箱內有a顆球的號碼小于40，有b顆球的號碼大于40，則關于a、b之值，下列何者正確？（　　）
A．a=16 B．a=24 C．b=24 D．b=34
組卷：1641引用：56難度：0.5
解析
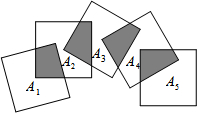4．如圖，將n個邊長都為2的正方形按如圖所示擺放，點A₁，A₂，…A_n分別是正方形的中心，則這n個正方形重疊部分的面積之和是（　　）
A．n B．n-1 C．（
1
4
）^n-1 D．
1
4
n
組卷：6333引用：81難度：0.7
解析
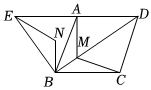5．如圖，四邊形ABCD是菱形，且∠ABC=60°，△ABE是等邊三角形，M為對角線BD（不含B點）上任意一點，將BM繞點B逆時針旋轉60°得到BN，連接EN、AM、CM，則下列五個結論中正確的是（　　）
①若菱形ABCD的邊長為1，則AM+CM的最小值1；
②△AMB≌△ENB；
③S_{四邊形AMBE}=S_{四邊形ADCM}；
④連接AN，則AN⊥BE；
⑤當AM+BM+CM的最小值為2
3
時，菱形ABCD的邊長為2．
A．①②③ B．②④⑤ C．①②⑤ D．②③⑤
組卷：2174引用：12難度：0.9
解析
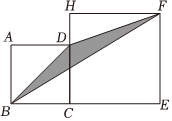6．如圖，正方形ABCD的邊長為2，H在CD的延長線上，四邊形CEFH也為正方形，則△DBF的面積為（　　）
A．4 B．
2
C．
2
2
D．2
組卷：1917引用：63難度：0.9
解析
7．已知過點（2，-3）的直線y=ax+b（a≠0）不經過第一象限，設s=a+2b,則s的取值范圍是（　　）
A．-5≤s≤-
3
2
B．-6＜s≤-
3
2
C．-6≤s≤-
3
2
D．-7＜s≤-
3
2
組卷：8353引用：64難度：0.5
解析

二、填空題（共10小題，每小題4分，滿分40分）

8．一次函數y=kx+b,當1≤x≤4時，3≤y≤6，則
b
k
的值是

．
組卷：6986引用：63難度：0.7
解析
9．已知一組數據x₁，x₂，…，x_n的方差是s²，則新的一組數據ax₁+1，ax₂+1，…，ax_n+1（a為非零常數）的方差是
（用含a和s²的代數式表示）．
組卷：365引用：7難度：0.9
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（共10小題，滿分89分）

26．對于坐標平面內的點，現將該點向右平移1個單位，再向上平移2個單位，這種點的運動稱為點A的斜平移，如點P（2，3）經1次斜平移后的點的坐標為（3，5），已知點A的坐標為（1，0）．
（1）分別寫出點A經1次，2次斜平移后得到的點的坐標．
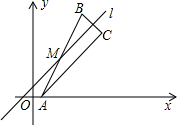
（2）如圖，點M是直線l上的一點，點A關于點M的對稱點為點B，點B關于直線l的對稱點為點C．
①若A、B、C三點不在同一條直線上，判斷△ABC是否是直角三角形？請說明理由．
②若點B由點A經n次斜平移后得到，且點C的坐標為（7，6），求出點B的坐標及n的值．
組卷：1174引用：4難度：0.3
解析
27．已知，矩形ABCD中，AB=4cm,BC=8cm,AC的垂直平分線EF分別交AD、BC于點E、F，垂足為O．
（1）如圖1，連接AF、CE．求證四邊形AFCE為菱形，并求AF的長；
（2）如圖2，動點P、Q分別從A、C兩點同時出發，沿△AFB和△CDE各邊勻速運動一周．即點P自A→F→B→A停止，點Q自C→D→E→C停止．在運動過程中，
①已知點P的速度為每秒5cm,點Q的速度為每秒4cm,運動時間為t秒，當A、C、P、Q四點為頂點的四邊形是平行四邊形時，求t的值．
②若點P、Q的運動路程分別為a、b（單位：cm,ab≠0），已知A、C、P、Q四點為頂點的四邊形是平行四邊形，求a與b滿足的數量關系式．
組卷：15713引用：95難度：0.3
解析