2022-2023學年天津六十一中九年級（下）段考數學試卷（一）

一、選擇題（本大題共12小題，每小題3分，共36分）

• 1．我國傳統文化中的“福祿壽喜”圖（如圖）由四個圖案構成．這四個圖案中既是軸對稱圖形，又是中心對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：677引用：29難度：0.9

  解析

• 2．在一個不透明的盒子里，裝有4個黑球和若干個白球，它們除顏色外無任何區別．搖勻后從中隨機摸出一個球記下顏色，再把它放回盒子中，不斷重復，共摸球100次，其中有25次摸到黑球，則估計盒子中大約有白球（　　）

  A．12個

  B．16個

  C．20個

  D．30個
  組卷：661引用：9難度：0.6

  解析

• 3．如圖，線段AB兩個端點的坐標分別為A（6，6），B（8，2），以原點O為位似中心，在第一象限內將線段AB縮小為原來的

  1

  2

  后得到線段CD，則點B的對應點D的坐標為（　　）

  A．（3，3）

  B．（1，4）

  C．（3，1）

  D．（4，1）
  組卷：422引用：5難度：0.7

  解析

• 4．對于拋物線y=3（x+2）²-1，下列判斷不正確的是（　　）

  A．拋物線的開口向上

  B．拋物線的頂點坐標為（-2，-1）

  C．對稱軸為直線x=-2

  D．若y隨x的增大而增大，則x＞2
  組卷：493引用：5難度：0.7

  解析

• 5．如圖，四邊形ABCD內接于⊙O，F是

  ?

  CD

  上一點，且

  ?

  DF

  =

  ?

  BC

  ，連接CF并延長交AD的延長線于點E，連接AC，若∠ABC=105°，∠BAC=25°，則∠E的度數為（　　）

  A．60°

  B．55°

  C．50°

  D．45°
  組卷：4933引用：36難度：0.7

  解析

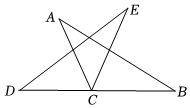• 6．如圖，將△ABC繞點C按逆時針方向旋轉至△DEC，使點D落在BC的延長線上．已知∠A=30°，∠B=35°，則∠ACE的大小是（　　）

  A．30°

  B．35°

  C．45°

  D．50°
  組卷：574引用：4難度：0.7

  解析

• 7．如圖所示，小正方形的邊長均為1，則下列選項中陰影部分的三角形與△ABC相似的是（　　）

  A．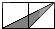

  B．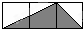

  C．

  D．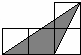
  組卷：6329引用：47難度：0.7

  解析

• 8．加工爆米花時，爆開且不糊的粒數的百分比稱為“可食用率”．在特定條件下，可食用率y與加工時間x（單位：min）滿足函數表達式y=-0.2x²+1.5x-2，則最佳加工時間為（　　）

  A．3min

  B．3.75min

  C．5min

  D．7.5min
  組卷：802引用：8難度：0.8

  解析

三、解答題（本大題共7小題，共66分）

• 24．（1）如圖1，點O是正方形ABCD兩條對角線的交點，分別延長OD到點G，OC到點E，使OG=2OD，OE=2OC，然后以OG、OE為鄰邊作正方形OEFG，連接AG、DE，則直線DE和AG的夾角為

  ；線段DE、AG之間的數量關系是

  ．
  
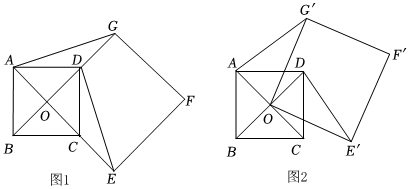
  （2）如圖2，正方形ABCD固定，將正方形OEFG繞點O逆時針旋轉α角（0°＜α＜360°）得到正方形OE'F'G'，
  ①試判斷（1）中的結論是否仍然成立？若成立，請證明你的結論；若不成立，請說明理由．
  ②若正方形ABCD的邊長為1時，在旋轉過程中，求AF'長的最大值和此時α角的度數，直接寫出結果不需要說明理由．
  組卷：84引用：2難度：0.1

  解析

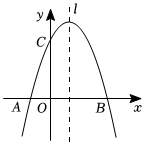• 25．如圖，已知拋物線y=ax²+bx+c經過A（-1，0），B（3，0），C（0，3）三點，直線l是拋物線的對稱軸．
  （1）求拋物線的函數關系式及對稱軸l；
  （2）設點P為直線l上的一個動點，當△PAC的周長最小時，求點P的坐標？
  （3）在直線l上是否存在點M，使△MAC為等腰三角形？若存在，求出點M的坐標；不存在，說明理由．
  組卷：379引用：4難度：0.1

  解析