當前位置：試卷中心 > 試卷詳情

2023-2024學年安徽省阜陽市潁上一中高二（上）開學數學試卷

發布：2024/8/3 8:0:9

一、單項選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求.

1．設集合A={x∈R||x-1|≤1}，
B
=
{
y
|
y
=
-
x
2
，-
2
≤
x
≤
1
}
，則?_R（A∩B）=（　　）
A．? B．{0} C．{x∈R|x≠0} D．R
組卷：350引用：2難度：0.5
解析
2．已知復數
z
=
3
+
i
1
-
i
（i為虛數單位），則z的共軛復數
z
=（　　）
A．1-2i B．2-4i C．1+2i D．2+4i
組卷：47引用：3難度：0.9
解析
3．已知
cos
（
π
6
-
α
）
=
1
3
，則
sin
（
5
π
6
+
α
）
cos
（
2
π
3
-
α
）
=（　　）
A．
-
8
9
B．
8
9
C．
-
2
2
9
D．
2
2
9
組卷：482引用：4難度：0.7
解析
4．某人從一魚池中捕得120條魚，做了記號之后，再放回池中，經過適當的時間后，再從池中捕得100條魚，結果發現有記號的魚為10條（假定魚池中不死魚，也不增加），則魚池中大約有魚（　　）
A．120條 B．1200條 C．130條 D．1000條
組卷：179引用：5難度：0.9
解析
5．命題“?x∈（1，2），log₂x-a＜0“為真命題的一個充分不必要條件是（　　）
A．a≥0 B．a≥2 C．a≥1 D．a≤4
組卷：91引用：13難度：0.7
解析
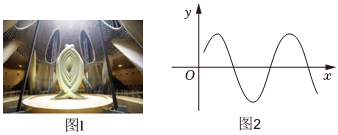6．阻尼器是一種以提供阻力達到減震效果的專業工程裝置．我國第一高樓上海中心大廈的阻尼器減震裝置，被稱為“定樓神器”，如圖1．由物理學知識可知，某阻尼器的運動過程可近似為單擺運動，其離開平衡位置的位移y（m）和時間t（s）的函數關系為y=sin（ωt+φ）（ω＞0，|φ|＜π），如圖2，若該阻尼器在擺動過程中連續三次到達同一位置的時間分別為t₁，t₂，t₃（0＜t₁＜t₂＜t₃），且t₁+t₂=2，t₂+t₃=5，則在一個周期內阻尼器離開平衡位置的位移大于0.5m的總時間為（　　）
A．
1
3
s
B．
2
3
s
C．1s D．
4
3
s
組卷：18引用：12難度：0.6
解析
7．若a＞b＞1，0＜c＜1，則（　　）
A．a^c＜b^c B．ab^c＜ba^c
C．log_ac＞log_bc D．alog_bc＞blog_ac
組卷：69引用：3難度：0.8
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本小題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

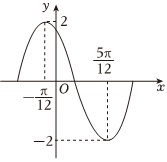21．已知函數f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的部分圖象如圖所示．
（1）求函數f（x）的解析式；
（2）若對
?
x
∈
（
0
，
π
2
）
，使得關于x的不等式
m
2
f
（
x
-
π
3
）
≤
co
s
2
2
x
-
m
+
1
恒成立，求實數m的最大值．
組卷：38引用：5難度：0.4
解析
22．已知函數
f
（
x
）
=
ln
（
x
2
+
a
+
x
）
的圖象關于原點對稱．
（1）求a的值；
（2）判斷f（x）的單調性；
（3）若x∈[0，1]，不等式f[（4^x+4^-x）+m]+f[m?（2^1+x-2^1-x）]＞0恒成立，求實數m的取值范圍．
組卷：65引用：1難度：0.5
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．a^c＜b^c	B．ab^c＜ba^c
C．log_ac＞log_bc	D．alog_bc＞blog_ac

2023-2024學年安徽省阜陽市潁上一中高二（上）開學數學試卷

一、單項選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求.

1．設集合A={x∈R||x-1|≤1}，B={y|y=-x2，-2≤x≤1}，則?R（A∩B）=（ ）

2．已知復數z=3+i1-i（i為虛數單位），則z的共軛復數z=（ ）

3．已知cos（π6-α）=13，則sin（5π6+α）cos（2π3-α）=（ ）

4．某人從一魚池中捕得120條魚，做了記號之后，再放回池中，經過適當的時間后，再從池中捕得100條魚，結果發現有記號的魚為10條（假定魚池中不死魚，也不增加），則魚池中大約有魚（ ）

5．命題“?x∈（1，2），log2x-a＜0“為真命題的一個充分不必要條件是（ ）

7．若a＞b＞1，0＜c＜1，則（ ）

四、解答題：本小題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

21．已知函數f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的部分圖象如圖所示．（1）求函數f（x）的解析式；（2）若對?x∈（0，π2），使得關于x的不等式m2f（x-π3）≤cos22x-m+1恒成立，求實數m的最大值．

22．已知函數f（x）=ln（x2+a+x）的圖象關于原點對稱．（1）求a的值；（2）判斷f（x）的單調性；（3）若x∈[0，1]，不等式f[（4x+4-x）+m]+f[m?（21+x-21-x）]＞0恒成立，求實數m的取值范圍．

1．設集合A={x∈R||x-1|≤1}，
B
=
{
y
|
y
=
-
x
2
，-
2
≤
x
≤
1
}
，則?_R（A∩B）=（　　）

2．已知復數
z
=
3
+
i
1
-
i
（i為虛數單位），則z的共軛復數
z
=（　　）

3．已知
cos
（
π
6
-
α
）
=
1
3
，則
sin
（
5
π
6
+
α
）
cos
（
2
π
3
-
α
）
=（　　）

4．某人從一魚池中捕得120條魚，做了記號之后，再放回池中，經過適當的時間后，再從池中捕得100條魚，結果發現有記號的魚為10條（假定魚池中不死魚，也不增加），則魚池中大約有魚（　　）

5．命題“?x∈（1，2），log₂x-a＜0“為真命題的一個充分不必要條件是（　　）

7．若a＞b＞1，0＜c＜1，則（　　）

22．已知函數
f
（
x
）
=
ln
（
x
2
+
a
+
x
）
的圖象關于原點對稱．
（1）求a的值；
（2）判斷f（x）的單調性；
（3）若x∈[0，1]，不等式f[（4^x+4^-x）+m]+f[m?（2^1+x-2^1-x）]＞0恒成立，求實數m的取值范圍．