2013-2014學年重慶市楊家坪中學高二（下）暑假數學作業（理科）（4）

一.選擇題（共8小題，每小題5分，共40分.在每小題列出的四個選項中，選出符合題目要求的一項）

• 1．已知集合A={x|x²-2x=0}，B={0，1，2}，則A∩B=（　　）

  A．{0}

  B．{0，1}

  C．{0，2}

  D．{0，1，2}
  組卷：1562引用：75難度：0.9

  解析

• 2．下列函數中，在區間（0，+∞）上為增函數的是（　　）

  A．y= x + 1	B．y=（x-1）2
  C．y=2-x	D．y=log0.5（x+1）
  組卷：3052引用：86難度：0.9

  解析

• 3．曲線

  x = - 1 + cosθ

  y = 2 + sinθ

  （θ為參數）的對稱中心（　　）

  A．在直線y=2x上	B．在直線y=-2x上
  C．在直線y=x-1上	D．在直線y=x+1上
  組卷：1579引用：23難度：0.9

  解析

• 4．當m=7，n=3時，執行如圖所示的程序框圖，輸出的S的值為（　　）
  

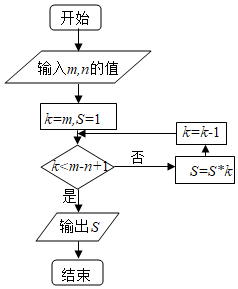
  A．7

  B．42

  C．210

  D．840
  組卷：3048引用：25難度：0.9

  解析

• 5．設{a_n}是公比為q的等比數列，則“q＞1”是“{a_n}為遞增數列”的（　　）

  A．充分而不必要條件	B．必要而不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：2573引用：51難度：0.7

  解析

• 6．若x,y滿足

  x + y - 2 ≥ 0

  kx - y + 2 ≥ 0

  y ≥ 0

  ，且z=y-x的最小值為-4，則k的值為（　　）

  A．2

  B．-2

  C． 1 2

  D．- 1 2
  組卷：2158引用：56難度：0.7

  解析

三．解答題（共6題，滿分67分）

• 19．已知橢圓C：x²+2y²=4，
  （1）求橢圓C的離心率；
  （2）設O為原點，若點A在橢圓C上，點B在直線y=2上，且OA⊥OB，求直線AB與圓x²+y²=2的位置關系，并證明你的結論．
  組卷：2156引用：11難度：0.1

  解析

• 20．對于數對序列P：（a₁，b₁），（a₂，b₂），…，（a_n，b_n），記T₁（P）=a₁+b₁，T_k（P）=b_k+max{T_k-1（P），a₁+a₂+…+a_k}（2≤k≤n），其中max{T_k-1（P），a₁+a₂+…+a_k}表示T_k-1（P）和a₁+a₂+…+a_k兩個數中最大的數，
  （Ⅰ）對于數對序列P：（2，5），（4，1），求T₁（P），T₂（P）的值；
  （Ⅱ）記m為a,b,c,d四個數中最小的數，對于由兩個數對（a,b），（c,d）組成的數對序列P：（a,b），（c,d）和P′：（c,d），（a,b），試分別對m=a和m=d兩種情況比較T₂（P）和T₂（P′）的大小；
  （Ⅲ）在由五個數對（11，8），（5，2），（16，11），（11，11），（4，6）組成的所有數對序列中，寫出一個數對序列P使T₅（P）最小，并寫出T₅（P）的值（只需寫出結論）．
  組卷：980引用：7難度：0.2

  解析