2022-2023學年湖南省長沙市雅禮中學高二（下）月考數學試卷（5月份）

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．若復數z滿足z（1+2i）=5，則z=（　　）

  A．1+i

  B．1-i

  C．1+2i

  D．1-2i
  組卷：69引用：6難度：0.8

  解析

• 2．已知

  p

  ：

  x

  -

  1

  x

  +

  2

  ≤

  0

  ，

  q

  ：-

  2

  ≤

  x

  ≤

  1

  ，則p是q的（　　）條件．

  A．充分不必要	B．必要不充分
  C．充要	D．既不充分也不必要
  組卷：821引用：5難度：0.7

  解析

• 3．若

  P

  （

  AB

  ）

  =

  1

  9

  ，

  P

  （

  A

  ）

  =

  2

  3

  ，

  P

  （

  B

  ）

  =

  1

  3

  ，則事件A與B的關系是（　　）

  A．事件A與B互斥

  B．事件A與B對立

  C．事件A與B相互獨立

  D．事件A與B既互斥又相互獨立
  組卷：788引用：14難度：0.8

  解析

• 4．函數f（x）=

  cos

  2

  x

  x

  2

  +

  1

  在[-π，π]上的大致圖象為（　　）

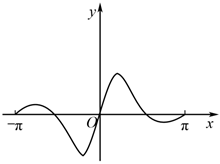
  A．	B．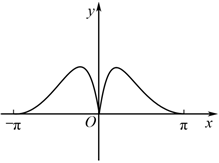
  C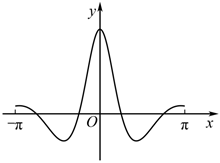．	D．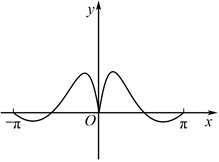
  組卷：150引用：10難度：0.8

  解析

• 5．關于函數

  y

  =

  lg

  1

  +

  x

  1

  -

  x

  ，下列說法不正確的是（　　）

  A．定義域為（-1，1）	B．圖像關于y軸對稱
  C．圖像關于原點對稱	D．在（0，1）內單調遞增
  組卷：148引用：2難度：0.6

  解析

• 6．已知某摩天輪的半徑為60m,其中心到地面的距離為70m,摩天輪啟動后按逆時針方向勻速轉動，每30分鐘轉動一圈．已知當游客距離地面超過100m時進入最佳觀景時間段，則游客在摩天輪轉動一圈的過程中最佳觀景時長約有（　　）

  A．5分鐘

  B．10分鐘

  C．15分鐘

  D．20分鐘
  組卷：252引用：7難度：0.6

  解析

• 7．已知x₁是函數f（x）=x+1-ln（x+2）的零點，x₂是函數g（x）=x²-2ax+4a+4的零點，且滿足|x₁-x₂|≤1，則實數a的最小值為（　　）

  A．-1

  B．-2

  C．2-2 2

  D．1-2 2
  組卷：266引用：5難度：0.5

  解析

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

• 21．設函數f（x）是定義域為R的偶函數，g（x）是定義域為R的奇函數，且f（x）+g（x）=2^x+1．
  （1）求f（x）與g（x）的解析式；
  （2）若h（x）=f（2x）-2mg（x）在[1，+∞）上的最小值為-2，求m的值．
  組卷：161引用：9難度：0.6

  解析

• 22．甲、乙兩名圍棋學員進行圍棋比賽，規定每局比賽勝者得1分，負者得0分，平局雙方均得0分，比賽一直進行到一方比另一方多兩分為止，多得兩分的一方贏得比賽．已知每局比賽中，甲獲勝的概率為α，乙獲勝的概率為β，兩人平局的概率為γ（α+β+γ=1，α＞0，β＞0，γ≥0），且每局比賽結果相互獨立．
  （1）若

  α

  =

  2

  5

  ，

  β

  =

  2

  5

  ，

  γ

  =

  1

  5

  ，求進行4局比賽后甲學員贏得比賽的概率；
  （2）當γ=0時，
  （i）若比賽最多進行5局，求比賽結束時比賽局數X的分布列及期望E（X）的最大值；
  （ii）若比賽不限制局數，寫出“甲學員贏得比賽”的概率（用α，β表示），無需寫出過程．
  組卷：424引用：7難度：0.4

  解析