當前位置：試卷中心 > 試卷詳情

2023年湖南師大附中高考數學三模試卷

發布：2024/6/22 8:0:10

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，有且只有一項符合題目要求；選對得5分，選錯得0分.

1．已知集合
A
=
{
x
|
x
-
1
x
-
4
＜
0
}
，B={x|x²-2x-3≥0}，則A∩B等于（　　）
A．（-1，1] B．（-∞，-1]∪（1，+∞）
C．[3，4） D．（-∞，-1]∪[3，+∞）
組卷：352引用：4難度：0.8
解析
2．若z=
1
-
i
1
+
i
+4-2i,則|z|=（　　）
A．5 B．4 C．3 D．2
組卷：163引用：5難度：0.8
解析
3．“b是
1
+
3
與
1
-
3
的等差中項”是“b是
2
+
3
與
2
-
3
的等比中項”的（　　）
A．充分不必要條件 B．必要不充分條件
C．充要條件 D．既不充分也不必要條件
組卷：178引用：5難度：0.8
解析
4．如圖，在△ABC中，AB=4，AC=2
2
，∠BAC=135°，D為邊BC的中點，且
AM
=
MD
，則向量
BM
的模為（　　）
A．
26
2
B．
5
2
2
C．
26
2
或
5
2
D．
26
2
或
5
2
2
組卷：584引用：3難度：0.7
解析
5．某網店經銷某商品，為了解該商品的月銷量y（單位：千件）與售價x（單位：元/件）之間的關系，收集5組數據進行了初步處理，得到如下數表：

x 5 6 7 8 9

y 8 6 4.5 3.5 3

根據表中的數據可得回歸直線方程
?
y
=-1.25x+13.75，以下說法正確的是（　　）
A．x,y具有負相關關系，相關系數r=-1.25
B．x每增加一個單位，y平均減少13.75個單位
C．第二個樣本點對應的殘差
?
e
2
=0.25
D．第三個樣本點對應的殘差
?
e
3
=-0.5
組卷：88引用：3難度：0.8
解析
6．已知函數
f
（
x
）
=
lo
g
2
x
2
?
lo
g
2
x
8
，若f（x₁）=f（x₂）（其中x₁≠x₂），則
1
x
1
+
9
x
2
的最小值為（　　）
A．
3
4
B．
3
2
C．2 D．4
組卷：1317引用：14難度：0.5
解析
7．已知平行六面體ABCD-A₁B₁C₁D₁的各棱長都為2，∠A₁AD=∠A₁AB=∠BAD=60°，E、F、G分別是棱AB、AD、CD的中點，則（　　）
A．B₁G∥平面A₁EF
B．平面A₁EF⊥平面ABCD
C．平面ABCD與平面A₁B₁C₁D₁間的距離為
6
3
D．直線AA₁與平面ABCD所成角的正弦值為
3
3
組卷：62引用：2難度：0.5
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

21．馬爾科夫鏈是概率統計中的一個重要模型，也是機器學習和人工智能的基石，在強化學習、自然語言處理、金融領域、天氣預測等方面都有著極其廣泛的應用．其數學定義為：假設我們的序列狀態是…，X_t-2，X_t-1，X_t，X_t+1，…，那么X_t+1時刻的狀態的條件概率僅依賴前一狀態X_t，即P（X_t+1|…，X_t-2，X_t-1，X_t）=P（X_t+1|X_t）．
現實生活中也存在著許多馬爾科夫鏈，例如著名的賭徒模型．
假如一名賭徒進入賭場參與一個賭博游戲，每一局賭徒賭贏的概率為50%，且每局賭贏可以贏得1元，每一局賭徒賭輸的概率為50%，且賭輸就要輸掉1元．賭徒會一直玩下去，直到遇到如下兩種情況才會結束賭博游戲：一種是手中賭金為0元，即賭徒輸光；一種是賭金達到預期的B元，賭徒停止賭博．記賭徒的本金為A（A∈N^*，A＜B），賭博過程如圖的數軸所示．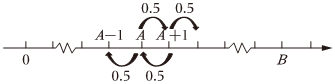

當賭徒手中有n元（0≤n≤B，n∈N）時，最終輸光的概率為P（n），請回答下列問題：
（1）請直接寫出P（0）與P（B）的數值．
（2）證明{P（n）}是一個等差數列，并寫出公差d.
（3）當A=100時，分別計算B=200，B=1000時，P（A）的數值，并結合實際，解釋當B→∞時，P（A）的統計含義．
組卷：1732引用：5難度：0.4
解析
22．已知函數f（x）=e^x-
a
x
（a∈R）．
（1）討論函數f（x）零點個數；
（2）若|f（x）|＞alnx-a恒成立，求a的取值范圍．
組卷：440引用：6難度：0.5
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．（-1，1]	B．（-∞，-1]∪（1，+∞）
C．[3，4）	D．（-∞，-1]∪[3，+∞）

A．充分不必要條件	B．必要不充分條件
C．充要條件	D．既不充分也不必要條件

x	5	6	7	8	9
y	8	6	4.5	3.5	3

2023年湖南師大附中高考數學三模試卷

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，有且只有一項符合題目要求；選對得5分，選錯得0分.

1．已知集合A={x|x-1x-4＜0}，B={x|x2-2x-3≥0}，則A∩B等于（ ）

2．若z=1-i1+i+4-2i,則|z|=（ ）

3．“b是1+3與1-3的等差中項”是“b是2+3與2-3的等比中項”的（ ）

4．如圖，在△ABC中，AB=4，AC=22，∠BAC=135°，D為邊BC的中點，且AM=MD，則向量BM的模為（ ）

6．已知函數f（x）=log2x2?log2x8，若f（x1）=f（x2）（其中x1≠x2），則1x1+9x2的最小值為（ ）

7．已知平行六面體ABCD-A1B1C1D1的各棱長都為2，∠A1AD=∠A1AB=∠BAD=60°，E、F、G分別是棱AB、AD、CD的中點，則（ ）

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

22．已知函數f（x）=ex-ax（a∈R）．（1）討論函數f（x）零點個數；（2）若|f（x）|＞alnx-a恒成立，求a的取值范圍．

1．已知集合
A
=
{
x
|
x
-
1
x
-
4
＜
0
}
，B={x|x²-2x-3≥0}，則A∩B等于（　　）

2．若z=
1
-
i
1
+
i
+4-2i,則|z|=（　　）

3．“b是
1
+
3
與
1
-
3
的等差中項”是“b是
2
+
3
與
2
-
3
的等比中項”的（　　）

4．如圖，在△ABC中，AB=4，AC=2
2
，∠BAC=135°，D為邊BC的中點，且
AM
=
MD
，則向量
BM
的模為（　　）

6．已知函數
f
（
x
）
=
lo
g
2
x
2
?
lo
g
2
x
8
，若f（x₁）=f（x₂）（其中x₁≠x₂），則
1
x
1
+
9
x
2
的最小值為（　　）

7．已知平行六面體ABCD-A₁B₁C₁D₁的各棱長都為2，∠A₁AD=∠A₁AB=∠BAD=60°，E、F、G分別是棱AB、AD、CD的中點，則（　　）

22．已知函數f（x）=e^x-
a
x
（a∈R）．
（1）討論函數f（x）零點個數；
（2）若|f（x）|＞alnx-a恒成立，求a的取值范圍．