人教新版九年級(jí)上冊(cè)《第22章 二次函數(shù)》2021年單元測(cè)試卷（11）

一、選擇題（本大題共10道小題）

• 1．下列函數(shù)中是二次函數(shù)的為（　　）

  A．y=3x-1	B．y=3x2-1
  C．y=（x+1）2-x2	D．y=x3+2x-3
  組卷：1888引用：25難度：0.9

  解析

• 2．對(duì)于二次函數(shù)y=-（x-1）²+2的圖象與性質(zhì)，下列說法正確的是（　　）

  A．對(duì)稱軸是直線x=1，最小值是2

  B．對(duì)稱軸是直線x=1，最大值是2

  C．對(duì)稱軸是直線x=-1，最小值是2

  D．對(duì)稱軸是直線x=-1，最大值是2
  組卷：6406引用：36難度：0.9

  解析

• 3．二次函數(shù)y=x²-（12-k）x+12，當(dāng)x＞1時(shí)，y隨著x的增大而增大，當(dāng)x＜1時(shí)，y隨著x的增大而減小，則k的值應(yīng)取（　　）

  A．12

  B．11

  C．10

  D．9
  組卷：2356引用：26難度：0.7

  解析

• 4．函數(shù)y=ax²-a與y=ax-a（a≠0）在同一坐標(biāo)系中的圖象可能是（　　）

  A．

  B．

  C．

  D．
  組卷：1173引用：16難度：0.9

  解析

• 5．若有二次函數(shù)y=ax²+c,當(dāng)x取x₁，x₂（x₁≠x₂）時(shí)，函數(shù)值相等，則當(dāng)x=x₁+x₂時(shí)，函數(shù)值為（　　）

  A．a(chǎn)+c

  B．a(chǎn)-c

  C．-c

  D．c
  組卷：1377引用：83難度：0.7

  解析

• 6．如圖，鉛球的出手點(diǎn)C距地面1米，出手后的運(yùn)動(dòng)路線是拋物線，出手后4秒鐘達(dá)到最大高度3米，則鉛球運(yùn)行路線的解析式為（　　）

  A．h=- 3 16 t2	B．h=- 3 16 t2+t
  C．h=- 1 8 t2+t+1	D．h=- 1 3 t2+2t+1
  組卷：1888引用：12難度：0.9

  解析

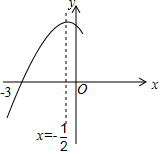• 7．如圖，拋物線y=ax²+bx+c（a≠0）與x軸交于點(diǎn)（-3，0），其對(duì)稱軸為直線x=-

  1

  2

  ，結(jié)合圖象分析下列結(jié)論：
  ①abc＞0；
  ②3a+c＞0；
  ③當(dāng)x＜0時(shí)，y隨x的增大而增大；
  ④一元二次方程cx²+bx+a=0的兩根分別為x₁=-

  1

  3

  ，x₂=

  1

  2

  ；
  ⑤

  b

  2

  -

  4

  ac

  4

  a

  ＜0；
  ⑥若m,n（m＜n）為方程a（x+3）（x-2）+3=0的兩個(gè)根，則m＜-3且n＞2，
  其中正確的結(jié)論有（　　）

  A．3個(gè)

  B．4個(gè)

  C．5個(gè)

  D．6個(gè)
  組卷：3320引用：15難度：0.6

  解析

• 8．已知拋物線y=ax²+bx+c（b＞a＞0）與x軸最多有一個(gè)交點(diǎn)，現(xiàn)有以下四個(gè)結(jié)論：
  ①該拋物線的對(duì)稱軸在y軸左側(cè)；
  ②關(guān)于x的方程ax²+bx+c+2=0無實(shí)數(shù)根；
  ③a-b+c≥0；
  ④

  a

  +

  b

  +

  c

  b

  -

  a

  的最小值為3．
  其中，正確結(jié)論的個(gè)數(shù)為（　　）

  A．1個(gè)

  B．2個(gè)

  C．3個(gè)

  D．4個(gè)
  組卷：8342引用：23難度：0.5

  解析

三、解答題（本大題共6道小題）

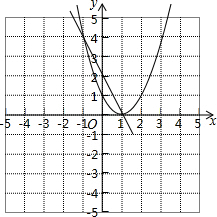• 23．設(shè)函數(shù)y=（x-1）[（k-1）x+（k-3）]（k是常數(shù)）．
  （1）當(dāng)k取1和2時(shí)的函數(shù)y₁和y₂的圖象如圖所示，請(qǐng)你在同一平面直角坐標(biāo)系中畫出當(dāng)k取0時(shí)的函數(shù)的圖象；
  （2）根據(jù)圖象，寫出你發(fā)現(xiàn)的一條結(jié)論；
  （3）將函數(shù)y₂的圖象向左平移4個(gè)單位，再向下平移2個(gè)單位，得到的函數(shù)y₃的圖象，求函數(shù)y₃的最小值．
  組卷：2920引用：55難度：0.5

  解析

• 24．如圖，某公路隧道橫截面為拋物線，其最大高度為6米，底部寬度OM為12米．現(xiàn)以O(shè)點(diǎn)為原點(diǎn)，OM所在直線為x軸建立直角坐標(biāo)系．
  （1）直接寫出點(diǎn)M及拋物線頂點(diǎn)P的坐標(biāo)；
  （2）求這條拋物線的解析式；
  （3）若要搭建一個(gè)矩形“支撐架”AD-DC-CB，使C、D點(diǎn)在拋物線上，A、B點(diǎn)在地面OM上，則這個(gè)“支撐架”總長(zhǎng)的最大值是多少？
  組卷：1174引用：43難度：0.1

  解析