2022-2023學(xué)年江西省南昌二中高一（下）期中數(shù)學(xué)試卷

一、單選題（本大題共8小題，共40分）

• 1．下列說法錯誤的是（　　）

  A．向量 CD 與向量 DC 長度相等

  B．單位向量都相等

  C．向量的模可以比較大小

  D．任一非零向量都可以平行移動
  組卷：817引用：10難度：0.9

  解析

• 2．若

  α

  ∈

  （

  π

  4

  ，

  π

  2

  ）

  ，則sinα，cosα，tanα的大小順序是（　　）

  A．cosα＜tanα＜sinα	B．tanα＜cosα＜sinα
  C．cosα＜sinα＜tanα	D．sinα＜cosα＜tanα
  組卷：21引用：2難度：0.7

  解析

• 3．在四邊形ABCD中，若

  AC

  =

  AB

  +

  AD

  ，則（　　）

  A．四邊形ABCD是平行四邊形

  B．四邊形ABCD是矩形

  C．四邊形ABCD是菱形

  D．四邊形ABCD是正方形
  組卷：241引用：9難度：0.8

  解析

• 4．sin20°cos70°+sin10°sin50°的值是（　　）

  A． 1 4

  B． 3 2

  C． 1 2

  D． 3 4
  組卷：474引用：8難度：0.9

  解析

• 5．已知tanα，tanβ是方程

  x

  2

  +

  3

  3

  x

  +

  4

  =

  0

  的兩根，且

  α

  ，

  β

  ∈

  （

  -

  π

  2

  ，

  π

  2

  ）

  ，則α+β=（　　）

  A． π 3

  B． π 3 或- 2 π 3

  C．- π 3 或 2 π 3

  D． - 2 π 3
  組卷：579引用：15難度：0.7

  解析

• 6．已知函數(shù)f（x）=Asin（ωx+φ）+k（A＞0，ω＞0，|φ|＜

  π

  2

  ）的部分圖象．如圖所示，將f（x）的圖象向右平移

  π

  6

  個單位長度后，得到函數(shù)g（x）的圖象，則g（x）在（

  π

  6

  ，

  2

  π

  3

  ）上的值域為（　　）
  

  A．（0，3]

  B．[-1，2）

  C．[-1，3]

  D．（-1，3）
  組卷：152引用：4難度：0.6

  解析

• 7．已知函數(shù)f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π）為偶函數(shù)，且f（x）+f（2-x）=0，當(dāng)ω取最小值時，f（x）的一個單調(diào)遞減區(qū)間是（　　）

  A．[0，1]

  B．[0，2]

  C．[0，π]

  D．[-π，0]
  組卷：164引用：3難度：0.6

  解析

四、解答題（本大題共6小題，共70分）

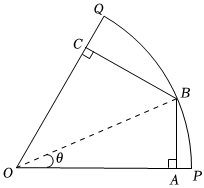• 21．如圖，扇形鋼板POQ的半徑為1m,圓心角為60°．現(xiàn)要從中截取一塊四邊形鋼板ABCO．其中頂點B在扇形POQ的弧

  ?

  PQ

  上，A，C分別在半徑OP，OQ上，且AB⊥OP，BC⊥OQ．
  （1）設(shè)∠AOB=θ，試用θ表示截取的四邊形鋼板ABCO的面積S（θ），并指出θ的取值范圍；
  （2）求當(dāng)θ為何值時，截取的四邊形鋼板ABCO的面積最大．
  組卷：174引用：13難度：0.6

  解析

• 22．已知函數(shù)

  f

  （

  x

  ）

  =

  3

  sinωxcosωx

  -

  si

  n

  2

  ωx

  +

  1

  2

  ，其中ω＞0，若實數(shù)x₁，x₂滿足|f（x₁）-f（x₂）|=2時，|x₁-x₂|的最小值為

  π

  2

  ．
  （Ⅰ）求ω的值及f（x）的單調(diào)遞減區(qū)間；
  （Ⅱ）若不等式

  f

  2

  （

  x

  ）

  +

  2

  acos

  （

  2

  x

  +

  π

  6

  ）

  -

  2

  a

  -

  2

  ＜

  0

  對任意

  x

  ∈

  （

  -

  π

  12

  ，

  π

  6

  ）

  時恒成立，求實數(shù)a應(yīng)滿足的條件．
  組卷：375引用：5難度：0.5

  解析