當前位置：試卷中心 > 試卷詳情

2022-2023學年河南省周口市項城第一高級中學高二（上）期末數學試卷

發布：2024/4/20 14:35:0

一.選擇題（共12小題，每小題5分，共60分）

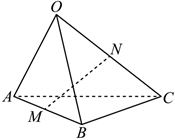1．已知三棱錐O-ABC中，點M，N分別為AB，OC的中點，且
OA
=
a
，
OB
=
b
，
OC
=
c
，則
NM
=（　　）
A．
1
2
（
b
+
c
-
a
）
B．
1
2
（
a
+
b
+
c
）
C．
1
2
（
a
-
b
+
c
）
D．
1
2
（
a
+
b
-
c
）
組卷：190引用：7難度：0.7
解析
2．如圖，圓x²+y²=8內有一點P₀（-1，2），AB為過點P₀的弦，若弦AB被點P₀平分時，則直線AB的方程是（　　）
A．x+2y+5=0 B．x-2y+5=0 C．x-2y-5=0 D．x+2y-15=0
組卷：67引用：3難度：0.7
解析
3．已知直線l₁：（m-2）x-3y-1=0與直線l₂：mx+（m+2）y+1=0相互平行，則實數m的值是（　　）
A．-4 B．1 C．-1 D．6
組卷：522引用：13難度：0.7
解析
4．已知雙曲線
x
2
a
2
-
y
2
=
1
的一個焦點與拋物線
y
2
=
4
3
x
的焦點相同，則雙曲線的漸近線方程是（　　）
A．
y
=±
2
x
B．y=±2x C．
y
=±
2
2
x
D．
y
=±
1
2
x
組卷：18引用：2難度：0.5
解析
5．設正項等比數列{a_n}的前n項和為S_n，若2S₃=3a₂+8a₁，則公比q=（　　）
A．2 B．
-
3
2
C．2或
-
3
2
D．2或
3
2
組卷：391引用：5難度：0.7
解析
6．已知函數f（x）=sin2x-xf'（0），則該函數的圖象在
x
=
π
2
處的切線方程為（　　）
A．3x+y-π=0 B．3x-y-π=0 C．x+3y-π=0 D．3x+y+π=0
組卷：520引用：6難度：0.7
解析
7．已知橢圓C₁：
x
2
a
2
+
y
2
b
2
=1（a＞b＞0）的左、右焦點分別為F₁，F₂，離心率為e₁，橢圓C₁的上頂點為M，且
M
F
1
?
M
F
2
=0．雙曲線C₂和橢圓C₁有相同焦點，且雙曲線C₂的離心率為e₂，P為曲線C₁與C₂的一個公共點，若∠F₁PF₂=
π
3
，則正確的是（　　）
A．
e
2
e
1
=2 B．e₁?e₂=
3
2
C．
e
2
1
+
e
2
2
=
5
2
D．
e
2
2
-
e
2
1
=1
組卷：1592引用：18難度：0.3
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三.解答題（共6小題，共70分）

21．已知雙曲線C：
x
2
a
2
-
y
2
b
2
=
1
（a＞0，b＞0）的焦點到漸近線的距離為2，漸近線的斜率為2．
（1）求雙曲線C的方程；
（2）設過點（0，2）的直線l與曲線C交于M，N兩點，問在y軸上是否存在定點P，使得
PM
?
PN
為常數？若存在，求出點P的坐標及此常數的值；若不存在，說明理由．
組卷：204引用：5難度：0.3
解析
22．已知函數f（x）=xlnx.
（Ⅰ）求曲線y=f（x）在點（e,f（e））處的切線方程；
（Ⅱ）求函數f（x）的最小值；
（Ⅲ）求函數g（x）=f（x）-1的零點個數，并說明理由．
組卷：202引用：3難度：0.7
解析