2022-2023學年湖北省黃岡市蘄春縣英才學校高二（上）期中數學試卷

一、單選題（本大題共8小題，每小題5分，共40分.）

• 1．若直線過兩點

  （

  1

  ，

  0

  ）

  ，

  （

  4

  ，

  3

  3

  ）

  ，則此直線的傾斜角是（　　）

  A．30°

  B．60°

  C．120°

  D．150°
  組卷：9引用：2難度：0.7

  解析

• 2．直線2x+（m+1）y-2=0與直線mx+3y-2=0平行，那么m的值是（　　）

  A．2

  B．-3

  C．2或-3

  D．-2或-3
  組卷：336引用：15難度：0.8

  解析

• 3．若動直線l經過點P（1，3），當點Q（3，-3）到直線l的距離最遠時，直線l的方程為（　　）

  A．3x+y-6=0

  B．3x+y+6=0

  C．x-3y+8=0

  D．x+3y-10=0
  組卷：150引用：2難度：0.7

  解析

• 4．已知四面體ABCD的所有棱長都等于a,E，F分別是棱AB，CD的中點，則

  EF

  ?

  AC

  等于（　　）

  A． - 1 4 a 2

  B． 1 4 a 2

  C． - 1 2 a 2

  D． 1 2 a 2
  組卷：53引用：2難度：0.7

  解析

• 5．圓心為（1，1）且過原點的圓的標準方程是（　　）

  A．（x-1）2+（y-1）2=1	B．（x+1）2+（y+1）2=1
  C．（x+1）2+（y+1）2=2	D．（x-1）2+（y-1）2=2
  組卷：4831引用：72難度：0.9

  解析

• 6．先后拋擲兩枚質地均勻的骰子，骰子朝上面的點數分別為a,b,構成一個基本事件（a,b）．記“這些基本事件中，滿足log_ba＞1”為事件E，則E發生的概率是（　　）

  A． 5 18

  B． 5 36

  C． 5 12

  D． 1 2
  組卷：94引用：2難度：0.7

  解析

• 7．在一次運動會男子羽毛球單打比賽中，運動員甲和乙進入了決賽．假設每局比賽中甲獲勝的概率為0.6，乙獲勝的概率為0.4，已知比賽規則是3局2勝制，則乙獲得冠軍的概率為（　　）

  A．0.288

  B．0.352

  C．0.648

  D．0.256
  組卷：188引用：5難度：0.6

  解析

四、解答題（本大題共6小題，第17題10分，其余各題每題12分，共70分.）

• 21．已知圓C經過點A（1，6）和B（-2，3），且圓心C在直線3x-y=0上．
  （1）求圓C的方程；
  （2）過點P（4，1）作圓C的切線，求切線方程．
  組卷：210引用：9難度：0.7

  解析

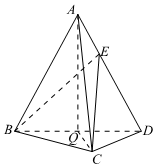• 22．如圖，在三棱錐A-BCD中，AB=AD，O為BD的中點，OA⊥CD．
  （1）證明：平面ABD⊥平面BCD；
  （2）若△OCD是邊長為1的等邊三角形，點E在棱AD上，DE=2EA，三棱錐B-ACD的體積為

  3

  3

  ，求平面BCD與平面BCE的夾角的余弦值．
  組卷：381引用：8難度：0.5

  解析