2022-2023學年重慶市主城區高三（上）第二次調研抽測數學試卷

一、選擇題：本大題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．已知集合M={-2，0，2}，N={-5，0，5}，T={-5，-2，2，5}，則（　　）

  A．M∩N=?

  B．M∪N=T

  C．（M∪N）∩T=T

  D．（M∩N）∪T=T
  組卷：84引用：5難度：0.7

  解析

• 2．已知復數z滿足z+3=4

  z

  +5i,i是虛數單位，則z²=（　　）

  A．-2i

  B．2i

  C．1+i

  D．1-i
  組卷：98引用：5難度：0.8

  解析

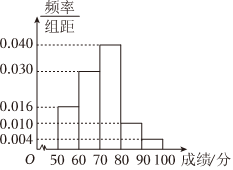• 3．如圖是根據某班學生在一次體能素質測試中的成績畫出的頻率分布直方圖，則由直方圖得到的80%分位數為（　　）

  A．75

  B．77.5

  C．78

  D．78.5
  組卷：151引用：4難度：0.7

  解析

• 4．正多面體統稱為柏拉圖體，被喻為最有規律的立體結構，其所有面都只由一種正多邊形構成（各面都是全等的正多邊形，且每個頂點所接的面數都一樣，各相鄰面所成的二面角都相等），正多面體共有5種，它們分別是正四面體、正六面體（即正方體）、正八面體、正十二面體、正二十面體．連接正方體中相鄰面的中心（如圖1），得到另一個柏拉圖體，即正八面體P-ABCD-Q（如圖2），設E，F，H分別為PA，PB，BC的中點，則下列說法正確的是（　　）
  

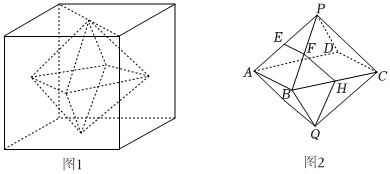
  A．AP與CQ為異面直線

  B．經過E，F，H的平面截此正八面體所得的截面為正五邊形

  C．平面PAB⊥平面PCD

  D．平面EFH∥平面PCD
  組卷：154引用：3難度：0.6

  解析

• 5．已知拋物線C：y²=2px（p＞0）與直線2x-y-4=0交于A，B兩點，且

  |

  AB

  |

  =

  3

  5

  ．若拋物線C的焦點為F，則|AF|+|BF|=（　　）

  A． 7 5

  B．7

  C．6

  D．5
  組卷：301引用：3難度：0.5

  解析

• 6．《數術記遺》是《算經十書》中的一部，相傳是漢末徐岳所著，該書記述了我國古代14種算法，分別是：積算（即籌算）、，太乙算、兩儀算、三才算、五行算、八卦算、九宮算、運籌算、了知算、成數算、把頭算、龜算、珠算和計數．某學習小組有甲、乙、丙、丁四人，該小組要收集九宮算、運籌算、了知算、成數算、把頭算、珠算6種算法的相關資料，要求每種算法只能一人收集，每人至少收集其中一種，則不同的分配方案種數有（　　）

  A．1560種

  B．2160種

  C．2640種

  D．4140種
  組卷：129引用：2難度：0.7

  解析

• 7．已知三棱錐P-ABC的頂點都在以PC為直徑的球M的球面上，PA⊥BC．若球M的表面積為48π，PA=4，則三棱錐P-ABC的體積的最大值為（　　）

  A． 16 3

  B． 32 3

  C． 64 3

  D．32
  組卷：95引用：2難度：0.6

  解析

四、解答題：本大題共6小題，共70分。解答應寫出文字說明，證明過程或演算步驟。

• 21．已知橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的離心率為

  1

  2

  ，左、右焦點分別為F₁，F₂，過F₁的直線y=t（x+1）交橢圓于M，N兩點，交y軸于P點，

  PM

  =

  λ

  M

  F

  1

  ，

  PN

  =

  μ

  NF

  1

  ，記△OMN，△OMF₂，△ONF₂的面積分別為S₁，S₂，S₃．
  （1）求橢圓C的標準方程；
  （2）若S₁=mS₂-λS₃，

  -

  3

  ≤

  μ

  ≤

  -

  4

  3

  ，求m的取值范圍．
  組卷：64引用：3難度：0.4

  解析

• 22．已知函數f（x）=lnx+

  a

  x

  -ax,函數g（x）=

  ln

  2

  x

  x

  +

  a

  e

  -

  x

  2

  x

  2

  -

  2

  a

  e

  x

  +1．
  （1）當a＞0時，求f（x）的單調區間；
  （2）已知a≥

  1

  2

  ，e^x＞

  1

  2

  x

  ，求證：g（x）＜0；
  （3）已知n為正整數，求證：

  1

  n

  +

  1

  n

  +

  1

  +

  1

  n

  +

  2

  +

  …

  +

  1

  2

  n

  -

  1

  +

  1

  2

  n

  ＞ln2．
  組卷：246引用：5難度：0.5

  解析