2023年山東省青島市高考數(shù)學二模試卷

一、單項選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．已知集合A={x|x²+2x-8＜0}，B={x|x=2n-1，n∈Z}，則A∩B=（　　）

  A．{-3，-1，1}

  B．{-1，1，3}

  C．（-4，2）

  D．（-2，4）
  組卷：97引用：2難度：0.9

  解析

• 2．已知O為坐標原點，復(fù)數(shù)z₁=1+i,z₂=2-i,z₃=1+mi（m∈R）分別表示向量

  OA

  ，

  OB

  ，

  OC

  ，若

  AB

  ⊥

  OC

  ，則|z₃|=（　　）

  A． 2

  B． 3

  C． 5 2

  D． 7 2
  組卷：87引用：2難度：0.7

  解析

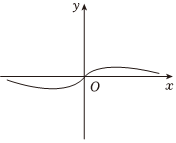• 3．已知函數(shù)f（x）=x,g（x）=2^x+2^-x，則大致圖象如圖的函數(shù)可能是（　　）

  A．f（x）+g（x）

  B．f（x）-g（x）

  C．f（x）g（x）

  D． f （ x ） g （ x ）
  組卷：325引用：6難度：0.7

  解析

• 4．某教育局為振興鄉(xiāng)村教育，將5名教師安排到3所鄉(xiāng)村學校支教，若每名教師僅去一所學校，每所學校至少安排1名教師，則不同的安排情況有（　　）

  A．300種

  B．210種

  C．180種

  D．150種
  組卷：208引用：3難度：0.7

  解析

• 5．在邊長為1的小正方形組成的網(wǎng)格中，△ABC如圖所示，則tanA=（　　）

  A． 7 4

  B．1

  C． 5 3

  D． 5 2
  組卷：97引用：5難度：0.7

  解析

• 6．已知O為坐標原點，直線l過拋物線D：y²=2px（p＞0）的焦點F，與D及其準線依次交于A，B，C三點（其中點B在A，C之間），若|AF|=4，|BC|=2|BF|．則△OAB的面積是（　　）

  A． 3

  B． 4 3 3

  C． 2 3

  D． 8 3 3
  組卷：149引用：3難度：0.4

  解析

• 7．三面角是立體幾何的基本概念之一，而三面角余弦定理是解決三面角問題的重要依據(jù)．三面角P-ABC是由有公共端點P且不共面的三條射線PA，PB，PC以及相鄰兩射線間的平面部分所組成的圖形，設(shè)∠APC=α，∠BPC=β，∠APB=γ，平面APC與平面BPC所成的角為θ，由三面角余弦定理得

  cosθ

  =

  cosγ

  -

  cosα

  ?

  cosβ

  sinα

  ?

  sinβ

  ．在三棱錐P-ABC中，PA=6，∠APC=60°，∠BPC=45°，∠APB=90°，PB+PC=6，則三棱錐P-ABC體積的最大值為（　　）

  A． 27 2 4

  B． 27 4

  C． 9 2

  D． 9 4
  組卷：183引用：3難度：0.4

  解析

四、解答題：本題共6小題，共70分。解答應(yīng)寫出文字說明，證明過程或演算步驟。

• 21．已知O為坐標原點，雙曲線

  C

  ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的左，右焦點分別為F₁，F(xiàn)₂，離心率等于

  6

  2

  ，點P是雙曲線C在第一象限上的點，直線PF₁與y軸的交點為Q，△PQF₂的周長等于6a,

  |

  P

  F

  1

  |

  2

  -

  |

  P

  F

  2

  |

  2

  =

  24

  ．
  （1）求C的方程；
  （2）過圓O：x²+y²=1上一點W（W不在坐標軸上）作C的兩條切線，對應(yīng)的切點為A，B．證明：直線AB與橢圓

  D

  ：

  x

  2

  4

  +

  y

  2

  =

  1

  相切于點T，且|WT|?|AB|=|WA|?|WB|．
  組卷：95引用：1難度：0.4

  解析

• 22．已知函數(shù)

  f

  （

  x

  ）

  =

  lnx

  -

  a

  （

  x

  -

  1

  x

  ）

  ，a＞0．
  （1）討論f（x）極值點的個數(shù)；
  （2）若f（x）恰有三個零點t₁，t₂，t₃（t₁＜t₂＜t₃）和兩個極值點x₁，x₂（x₁＜x₂）．
  （ⅰ）證明：f（x₁）+f（x₂）=0；
  （ⅱ）若m＜n,且mlnm=nlnn,證明：

  （

  1

  -

  m

  ）

  e

  -

  m

  t

  1

  t

  2

  t

  3

  ＞

  n

  （

  lnn

  +

  1

  ）

  ．
  組卷：275引用：7難度：0.6

  解析