2023-2024學年上海市青浦高級中學高一（上）質檢數學試卷（10月份）

一、填空題（本大題共12小題，滿分36分，每小題3分，考生應在答題紙相應編號的空格內直接填寫結果，每個空格填對得3分，否則一律得零分）

• 1．若全集U=R，集合A=（-2，+∞），則

  A

  =

  ．
  組卷：9引用：3難度：0.8

  解析

• 2．已知集合A={x|0＜x＜2}，B={x|-1＜x＜1}，則A∪B=

  ．
  組卷：280引用：6難度：0.9

  解析

• 3．已知x²∈{0，1，x}，則實數x的值是

   

  ．
  組卷：680引用：13難度：0.9

  解析

• 4．設集合M={x|-1≤x＜2}，N={x|x-k≤0}，若M∩N=?，則k的取值范圍是

  ．
  組卷：898引用：8難度：0.5

  解析

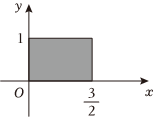• 5．用描述法表示如圖中陰影部分的點（含邊界）的集合

  ．
  組卷：88引用：5難度：0.8

  解析

• 6．已知m∈R，若關于x的方程2mx²+3x+m-1=m²?x²+（m+1）x+1解集為R，則m的值為

  ．
  組卷：131引用：3難度：0.8

  解析

• 7．設三元集合

  {

  a

  ,

  b

  a

  ，

  1

  }

  =

  {

  a

  2

  ，

  a

  +

  b

  ,

  0

  }

  ，則a²⁰²³+b²⁰²⁴=

  ．
  組卷：33引用：2難度：0.8

  解析

三、解答題（本大題共有5題，滿分52分，解答下列各題必須在答題紙相應編號的規定區域內寫出必要的步驟）

• 20．已知x₁，x₂是一元二次方程4kx²-4kx+k+1=0的兩個不同實數根．
  （1）是否存在實數k,使

  （

  2

  x

  1

  -

  x

  2

  ）

  （

  x

  1

  -

  2

  x

  2

  ）

  =

  3

  4

  成立？若存在，求出k的值；若不存在，請說明理由；
  （2）求使

  x

  1

  x

  2

  +

  x

  2

  x

  1

  -

  2

  的值為整數的實數k的整數值．
  組卷：12引用：4難度：0.6

  解析

• 21．已知n為正整數，集合A={α|α=（x₁，x₂，…，x_2n），x_i∈{-1，1}，i=1，2，…，2n}具有性質P：“對于集合A中的任意元素α=（x₁，x₂，…，x_2n），x₁+x₂+…+x_2n=0，且x₁+x₂+…+x_i≥0，其中i=1，2，…，2n-1”．
  （1）當n=3時，寫出滿足條件的集合A；
  （2）當n=9時，求x₁+x₂+…+x₉的所有可能的取值．
  組卷：96引用：4難度：0.5

  解析