2022-2023學年北京交大附中高一（下）期中數學試卷

一、選擇題：本大題共10小題，每小題4分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知α∈

  （

  π

  2

  ，

  π

  ）

  ，且sinα=

  3

  5

  ，則tanα=（　　）

  A． 3 4

  B． - 3 4

  C． 4 3

  D． - 4 3
  組卷：993引用：10難度：0.8

  解析

• 2．已知向量

  a

  =（t,1），

  b

  =（1，2）．若

  a

  ⊥

  b

  ，則實數t的值為（　　）

  A．-2

  B．2

  C． - 1 2

  D． 1 2
  組卷：410引用：10難度：0.7

  解析

• 3．如圖，角α以Ox為始邊，它的終邊與單位圓O相交于點P，且點P的橫坐標為

  3

  5

  ，則

  sin

  （

  π

  2

  +

  α

  ）

  的值為（　　）

  A． - 3 5

  B． 3 5

  C． - 4 5

  D． 4 5
  組卷：890引用：9難度：0.7

  解析

• 4．向量

  a

  ，

  b

  ，

  c

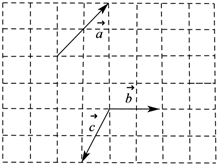  在邊長為1的正方形網格中的位置如圖所示，則

  （

  a

  -

  b

  ）

  ?

  c

  =（　　）

  A．-4

  B．4

  C．2

  D．-8
  組卷：654引用：7難度：0.7

  解析

• 5．已知向量

  a

  ，

  b

  滿足|

  a

  |=1，

  b

  =（-2，1），且|

  a

  -

  b

  |=2，則

  a

  ?

  b

  =（　　）

  A．-1

  B．0

  C．1

  D．2
  組卷：922引用：8難度：0.7

  解析

• 6．設函數

  f

  （

  x

  ）

  =

  sin

  （

  ωx

  -

  π

  6

  ）

  +

  k

  （

  ω

  ＞

  0

  ）

  ，若

  f

  （

  x

  ）

  ≤

  f

  （

  π

  3

  ）

  對任意的實數x都成立，則ω的一個可取值為（　　）

  A．4

  B．5

  C．7

  D．8
  組卷：166引用：2難度：0.7

  解析

三、解答題：本大題共4小題，共40分.解答應寫出文字說明，證明過程或演算步驟.

• 18．已知函數f（x）=sin²x+3cosx+3，（x∈R）．
  （1）判斷函數f（x）的奇偶性并說明理由；
  （2）求f（x）的最小值并指出函數取得最小值時x的值；
  （3）直接寫出函數f（x）在[0，2π]上的零點．
  組卷：76引用：1難度：0.5

  解析

• 19．已知函數f（x）的定義域為R，若存在常數T≠0，使得f（x）=Tf（x+T）對任意的x∈R成立，則稱函數f（x）是Ω函數．
  （1）判斷函數F（x）=x,h（x）=sinπx是否是Ω函數，不必說明理由；
  （2）若函數f（x）是Ω函數，且f（x）是偶函數，求證：函數f（x）是周期函數；
  （3）若函數f（x）=sinkx是Ω函數．求實數k的取值范圍；
  （4）定義域為R的函數g（x）同時滿足以下三條性質：
  ①存在x₀∈R，使得g（x₀）≠0；
  ②對于任意x∈R，有g（x+2）=9g（x）．
  ③f（x）不是單調函數，但是它圖像連續不斷，
  寫出滿足上述三個性質的一個函數g（x），則g（x）=_____．（不必說明理由）
  組卷：33引用：1難度：0.5

  解析