2023年江蘇省泰州市靖江市濱江學校中考數學三模試卷
發布：2024/7/3 8:0:9
一、選擇題（本大題共6小題，每小題3分，滿分18分，在每小題所給出的四個選項中，恰有一項是符合題目要求的，選擇正確選項的字母代號涂在答題卡相應的位置上）
-
1．計算-2-2的結果是（ ）
組卷：147引用：31難度：0.9 -
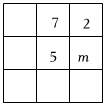2．幻方是相當古老的數學問題，我國古代的《洛書》中記載了最早的幻方——九宮圖．將數字1～9分別填入如圖所示的幻方中，要求每一橫行、每一豎行以及兩條斜對角線上的數字之和都是15，則m的值為（ ）組卷：258引用：7難度：0.7 -
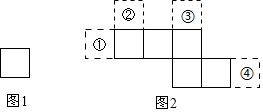3．圖1和圖2中所有的正方形都全等，將圖1的正方形放在圖2中的①②③④某一位置，所組成的圖形不能圍成正方體的位置是（ ）組卷：869引用：7難度：0.9 -
4．如圖，為了估算河的寬度，在河對岸選定一個目標點A，在近岸取點B，C，D，E，使得A，B與C共線，A，D與E共線，且直線AC與河岸垂直，直線BD，CE均與直線AC垂直．經測量，得到BC，CE，BD的長度，設AB的長為x,則下列等式成立的是（ ）組卷：546引用：7難度：0.7 -
5．已知x1、x2是關于x的方程x2-2x-m2=0的兩根，下列結論中不一定正確的是（ ）
組卷：1197引用：10難度：0.6 -
6．從A地到B地有駕車、公交、地鐵三種出行方式，為了選擇適合的出行方式，對6：00-10：00時段這三種出行方式不同出發時刻所用時長（從A地到B地）進行調查、記錄與整理，數據如圖所示．
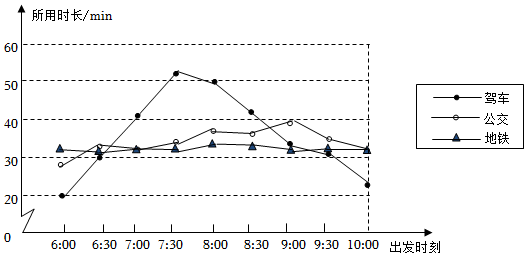
根據統計圖提供的信息，下列推斷合理的是（ ）組卷：797引用：10難度：0.8
二、填空題（本大題共有10小題，每小題3分，共30分．請把答案直接寫在答題卷相應位置上）
-
7．點M（2，-3）到x軸的距離是 ．
組卷：547引用：22難度：0.7 -
8．已知∠A比它的補角大40°，則∠A度數是．
組卷：328引用：4難度：0.9
三、解答題（共10小題，滿分102分）
-
25．【概念認識】定義：對角線互相垂直且相等的四邊形叫做垂等四邊形．
（1）如圖1，已知在垂等四邊形ABCD中，對角線AC與BD交于點E，若AB⊥AD，AB=4cm,cos∠ABD=，則AC的長度=cm.45
【數學理解】（2）在探究如何畫“圓內接垂等四邊形”的活動中，小李想到可以利用八年級的所學三角形全等．如圖2，在⊙O中，已知AB是弦，OA、OB是半徑，求作：⊙O的內接垂等四邊形ABCD．（要求：尺規作圖，不寫作法，保留痕跡）
【問題解決】（3）如圖3，已知A是⊙O上一定點，B為⊙O上一動點，以AB為一邊作出⊙O的內接垂等四邊形（A、B不重合且A、B、O三點不共線），對角線AC與BD交于點E，⊙O的半徑為2，當點E到AD的距離為2時，求弦AB的長度．3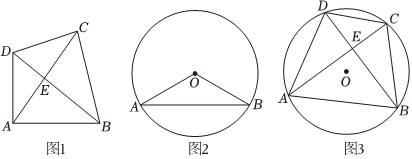
組卷：453引用：1難度：0.5 -
26．定義：對于關于x的函數y,我們稱函數y'=
，為函數y的n分函數（其中n為常數）．例如：一次函數y=x+4的3分函數為y'=y（x≤n）-y（x＞n）．x+4（x≤3）-x-4（x＞3）
（1）已知點P（4，n）在一次函數y=-2x+1的2分函數圖象上，求n的值．
（2）若y′是反比例函數y=的3分函數，當1≤x≤5時，求y′的取值范圍．3x
（3）已知（a,b）是二次函數y=x2-x-6的1分函數圖象上的點，當-1＜a≤k時，滿足-≤b＜6，則k的最大值為．254
（4）若點M、N的坐標分別為（m-2，1）、（m+3，1），連接MN．當二次函數y=x2-2x-3的m分函數圖象與線段MN有兩個公共點時，直接寫出m的取值范圍．組卷：452引用：2難度：0.2