當前位置：試卷中心 > 試卷詳情

2022-2023學年江西省部分學校高二（上）第一次月考數學試卷（10月份）

發布：2024/7/20 8:0:8

一、選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題

1．傾斜角為120°的直線經過點（a+1，3）和（2a-2，3a），則a=（　　）
A．
-
3
B．
3
C．3 D．-3
組卷：74引用：4難度：0.8
解析
2．橢圓
x
2
5
+
y
2
9
=
1
上的一點到兩個焦點的距離之和為（　　）
A．
2
5
B．4 C．6 D．18
組卷：68引用：5難度：0.7
解析
3．雙曲線C：
x
2
36
-
y
2
13
=1上的點P到左焦點的距離為10，則P到右焦點的距離為（　　）
A．2 B．22 C．2或22 D．12
組卷：287引用：5難度：0.8
解析
4．圓x²+y²-4x=0與圓（x-a）²+（y+3）²=9恰有兩條公切線，則a的取值范圍是（　　）
A．（-2，6） B．（-4，4） C．（-5，5） D．（-6，6）
組卷：514引用：5難度：0.8
解析
5．已知直線
l
：
3
x
+
y
-
2
=
0
，則（　　）
A．直線l的傾斜角為
5
π
6
B．直線l的斜率為
3
C．直線l的一個法向量為
u
=
（
1
，
3
）
D．直線l的一個方向向量為
v
=
（
-
3
，
3
）
組卷：87引用：8難度：0.7
解析
6．已知雙曲線
C
：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的左，右焦點分別為F₁，F₂，P是右支上一點，且|PF₁|=6|PF₂|，則雙曲線C的離心率的取值范圍是（　　）
A．
（
0
，
7
5
]
B．
（
1
，
4
3
]
C．
（
1
，
7
5
]
D．
[
7
5
，
+
∞
）
組卷：607引用：4難度：0.5
解析
7．如圖，已知雙曲線
C
：
x
2
a
2
-
y
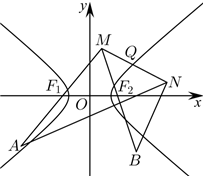2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的左、右焦點分別為F₁，F₂，點M與C的焦點不重合，點M關于F₁，F₂的對稱點分別為A，B，線段MN的中點Q在C的右支上．若|AN|-|BN|=18，則C的實軸長為（　　）
A．6 B．9 C．12 D．15
組卷：177引用：3難度：0.8
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟。

21．已知橢圓C：
x
2
a
2
+
y
2
a
2
-
4
=1（a＞2）過點（
5
4
，
9
4
），F₁，F₂分別為左、右焦點，P為第一象限內橢圓C上的動點，直線PF₁，PF₂與直線x=t（t＞0）分別交于A，B兩點，記△PAB和△PF₁F₂的面積分別為S₁，S₂．
（1）試確定實數t的值，使得點P到F₂的距離與到直線x=t的距離之比為定值k,并求出k的值；
（2）在（1）的條件下，若
S
1
S
2
=
25
9
，求
|
PA
|
|
P
F
1
|
|
PB
|
|
P
F
2
|
的值．
組卷：163引用：6難度：0.5
解析
22．已知從曲線
C
：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的左、右焦點分別為F₁，F₂，實軸長為
2
3
、一條漸近線方程為
3
x
-
3
y
=
0
，過F₂的直線l與雙曲線C的右支交于A，B兩點．
（1）求雙曲線C的方程；
（2）已知
P
（
-
5
，
0
）
，若△ABP的外心Q的橫坐標為0，求直線l的方程．
組卷：91引用：7難度：0.4
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

2022-2023學年江西省部分學校高二（上）第一次月考數學試卷（10月份）

一、選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題

1．傾斜角為120°的直線經過點（a+1，3）和（2a-2，3a），則a=（ ）

2．橢圓x25+y29=1上的一點到兩個焦點的距離之和為（ ）

3．雙曲線C：x236-y213=1上的點P到左焦點的距離為10，則P到右焦點的距離為（ ）

4．圓x2+y2-4x=0與圓（x-a）2+（y+3）2=9恰有兩條公切線，則a的取值范圍是（ ）

5．已知直線l：3x+y-2=0，則（ ）

6．已知雙曲線C：x2a2-y2b2=1（a＞0，b＞0）的左，右焦點分別為F1，F2，P是右支上一點，且|PF1|=6|PF2|，則雙曲線C的離心率的取值范圍是（ ）

7．如圖，已知雙曲線C：x2a2-y2b2=1（a＞0，b＞0）的左、右焦點分別為F1，F2，點M與C的焦點不重合，點M關于F1，F2的對稱點分別為A，B，線段MN的中點Q在C的右支上．若|AN|-|BN|=18，則C的實軸長為（ ）

四、解答題：本題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟。

1．傾斜角為120°的直線經過點（a+1，3）和（2a-2，3a），則a=（　　）

2．橢圓
x
2
5
+
y
2
9
=
1
上的一點到兩個焦點的距離之和為（　　）

3．雙曲線C：
x
2
36
-
y
2
13
=1上的點P到左焦點的距離為10，則P到右焦點的距離為（　　）

4．圓x²+y²-4x=0與圓（x-a）²+（y+3）²=9恰有兩條公切線，則a的取值范圍是（　　）

5．已知直線
l
：
3
x
+
y
-
2
=
0
，則（　　）

6．已知雙曲線
C
：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的左，右焦點分別為F₁，F₂，P是右支上一點，且|PF₁|=6|PF₂|，則雙曲線C的離心率的取值范圍是（　　）

7．如圖，已知雙曲線
C
：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的左、右焦點分別為F₁，F₂，點M與C的焦點不重合，點M關于F₁，F₂的對稱點分別為A，B，線段MN的中點Q在C的右支上．若|AN|-|BN|=18，則C的實軸長為（　　）