2022-2023學(xué)年北京二中高一（下）第六次段考數(shù)學(xué)試卷
發(fā)布：2024/7/1 8:0:9
選擇題
-
1．若復(fù)數(shù)z滿(mǎn)足（1+i）z=|1+i|，則復(fù)數(shù)
的虛部是（ ）z組卷：236引用：8難度：0.8 -
2．某校“校園歌手”比賽中，某選手獲得的原始評(píng)分為x1，x2，x3，x4，x5，x6，x7，去掉一個(gè)最高分和一個(gè)最低分后得到有效評(píng)分，則有效評(píng)分與原始評(píng)分相比較，一定不變的特征數(shù)是（ ）
組卷：86引用：3難度：0.8 -
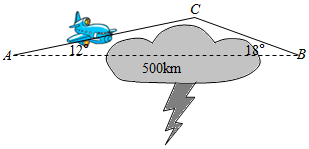3．如圖，一架飛機(jī)從A地飛往B地，兩地相距500km.行員為了避開(kāi)某一區(qū)域的雷雨云層，從A點(diǎn)起飛以后，就沿與原來(lái)的飛行方向AB成12°角的方向飛行，飛行到中途C點(diǎn)，再沿與原來(lái)的飛行方向AB成18°角的方向繼續(xù)飛行到終點(diǎn)B點(diǎn)．這樣飛機(jī)的飛行路程比原來(lái)的路程500km大約多飛了（ ）（sin12°≈0.21，sin18°≈0.31）組卷：204引用：12難度：0.7 -
4．甲、乙、丙三名射箭運(yùn)動(dòng)員在某次測(cè)試中各射箭20次，三人的測(cè)試成績(jī)?nèi)缦卤恚?table class="edittable">
甲的成績(jī) 環(huán)數(shù) 7 8 9 10 頻數(shù) 5 5 5 5 乙的成績(jī) 環(huán)數(shù) 7 8 9 10 頻數(shù) 6 4 4 6
若s1，s2，s3分別表示甲、乙、丙三名運(yùn)動(dòng)員這次測(cè)試成績(jī)的標(biāo)準(zhǔn)差，則有（ ）丙的成績(jī) 環(huán)數(shù) 7 8 9 10 頻數(shù) 4 6 6 4 組卷：76引用：1難度：0.8 -
5．已知α，β，γ是三個(gè)不同的平面，m,n是兩條不同的直線，若α∩γ=m,β∩γ=n,則“m∥n”是“α∥β”的（ ）
組卷：45引用：2難度：0.7 -
6．在正方體ABCD-A1B1C1D1中，M是AD的中點(diǎn)，N是C1D1的中點(diǎn)，則異面直線D1M與DN所成角的余弦值為（ ）
組卷：281引用：8難度：0.7 -
7．經(jīng)緯度是經(jīng)度與緯度的合稱(chēng)，它們組成一個(gè)坐標(biāo)系統(tǒng)，稱(chēng)為地理坐標(biāo)系統(tǒng)，它是利用三維空間的球面來(lái)定義地球上的空間的球面坐標(biāo)系能夠標(biāo)示地球上任何一個(gè)位置，其中緯度是地球重力方向上的鉛垂線與赤道平面所成的線面角．如世界最高峰珠穆朗瑪峰就處在北緯30°，若將地球看成近似球體，其半徑約為6400km,則北緯30°緯線的長(zhǎng)為（ ）
組卷：202引用：6難度：0.6
三、解答題
-
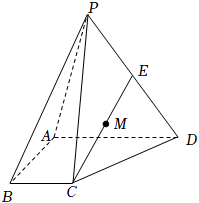22．如圖，在四棱錐P-ABCD中，平面PAD⊥平面ABCD，BC∥平面，∠ABC=90°，E是PD的中點(diǎn)．PAD，BC=12AD
（1）求證：BC∥AD；
（2）求證：平面PAB⊥平面PAD；
（3）若M是線段CE上任意一點(diǎn)，試判斷線段AD上是否存在點(diǎn)N，使得MN∥平面PAB？請(qǐng)說(shuō)明理由．組卷：1132引用：7難度：0.8 -
23．已知集合S={1，2，?，n}（n≥3且n∈N*），A={a1，a2，…，am}，且A?S．若對(duì)任意ai∈A，aj∈A（1≤i≤j≤m），當(dāng)ai+aj≤n時(shí)，存在ak∈A（1≤k≤m），使得ai+aj=a4，則稱(chēng)A是S的m元完美子集．
（1）判斷下列集合是否是S={1，2，3，4，5}的3元完美子集，并說(shuō)明理由；
①A1={1，2，4}；②A2={2，4，5}
（2）若A={a1，a2，a3}是S={1，2，…，7}的3元完美子集，求a1+a2+a3的最小值；
（3）若A={a1，a2，…，am}是S={1，2，…，n}（n≥3且n∈N*）的m元完美子集，求證：a1+a2+?+am≥．m（n+1）2組卷：65引用：2難度：0.3