2022-2023學年安徽省合肥七中高一（下）期中數學試卷

一、單選題（本大題共8小題，每小題5分，共40分，每小題只有一個正確答案）

• 1．復平面內表示復數

  z

  =

  1

  -

  i

  i

  的點位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：93引用：12難度：0.8

  解析

• 2．若平面向量

  a

  與

  b

  的夾角為60°，

  a

  =

  （

  2

  ，

  0

  ）

  ，

  |

  b

  |

  =

  1

  ，則

  |

  a

  +

  2

  b

  |

  等于（　　）

  A． 3

  B． 2 3

  C．4

  D．12
  組卷：1318引用：24難度：0.7

  解析

• 3．攢尖是古代中國建筑中屋頂的一種結構形式，依其平面有圓形攢尖、三角攢尖、四角攢尖、六角攢尖等，多見于亭閣式建筑．如故宮中和殿的屋頂為四角攢尖頂，它的主要部分的輪廓可近似看作一個正四棱錐，設正四棱錐的側面等腰三角形的頂角為60°，則該正四棱錐的側面積與底面積的比為（　　）

  A． 3 4

  B． 3 3

  C． 3 2

  D． 3
  組卷：220引用：6難度：0.6

  解析

• 4．定慧禪寺位于江蘇省如皋市，是國家AAA級旅游景區．地處如皋古城東南隅，寺門正對玉帶河，東臨放生池，西南傍玉蓮池，寺院平面布置呈“回“字形，樓堂環繞四周，寶殿坐落中央，形成“水環寺，樓抱殿“獨特格局．某同學為測量寺內觀音塔的高度MN，在觀音塔的正北方向找到一座建筑物AB，高約為22.5m,在地面上點C處（B，C，N三點共線）測得建筑物頂部A，觀音塔頂部M的仰角分別為30°和45°，在A處測得觀音塔頂部M的仰角為15°，觀音塔的高度約為（　　）
  

  A．32m

  B．39m

  C．45m

  D．55m
  組卷：169引用：4難度：0.5

  解析

• 5．已知圓臺的母線長為4，上底面圓和下底面圓半徑的比為1：3，其側面展開圖所在扇形的圓心角為

  π

  2

  ，則圓臺的高為（　　）

  A． 2 3

  B． 15

  C．4

  D． 3 2
  組卷：312引用：2難度：0.7

  解析

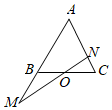• 6．如圖所示，在△ABC中，點O是BC的中點，過點O的直線分別交直線AB、AC于不同的兩點M、N，若

  AB

  =m

  AM

  ，

  AC

  =n

  AN

  （m,n＞0），則

  1

  m

  +

  4

  n

  的最小值為（　　）

  A．2

  B．3

  C． 9 2

  D．5
  組卷：609引用：9難度：0.7

  解析

• 7．△ABC中，已知（b+c）sin（A+C）=（a+c）（sinA-sinC），設D是BC邊的中點，且△ABC的面積為

  3

  ，則

  AB

  ?

  （

  DA

  +

  DB

  ）

  等于（　　）

  A．2

  B．4

  C．-4

  D．-2
  組卷：124引用：4難度：0.7

  解析

三、解答題（本大題共6小題，共70分）

• 21．如圖，某小區準備將閑置的一直角三角形地塊開發成公共綠地，圖中

  ∠

  B

  =

  π

  2

  ，

  AB

  =

  a

  ,

  BC

  =

  3

  a

  ．設計時要求綠地部分（如圖中陰影部分所示）有公共綠地走道MN，且兩邊是兩個關于走道MN對稱的三角形（△AMN和△A'MN）．現考慮方便和綠地最大化原則，要求點M與點A，B均不重合，A'落在邊BC上且不與端點B，C重合，設∠AMN=θ．
  （1）若

  θ

  =

  π

  3

  ，求此時公共綠地的面積；
  （2）為方便小區居民的行走，設計時要求AN，A'N的長度最短，求此時綠地公共走道MN的長度．
  組卷：587引用：9難度：0.3

  解析

• 22．在平面直角坐標系中，已知

  A

  （

  t

  ,

  2

  t

  ）

  ，

  B

  （

  8

  -

  m

  ,

  8

  -

  3

  2

  m

  ）

  ，

  C

  （

  7

  -

  m

  ,

  0

  ）

  ，t,m∈R，t≠0．
  （1）若t=1，m=4，P為x軸上的一動點，點A'（1，-2）．
  （ⅰ）當A'，P，B三點共線時，求點P的坐標；
  （ⅱ）求

  |

  PA

  |

  +

  |

  PB

  |

  的最小值；
  （2）若t=sinθ，θ∈（0，π），且

  CA

  與

  CB

  的夾角

  α

  ∈

  [

  0

  ，

  π

  2

  ）

  ，求m的取值范圍．
  組卷：182引用：6難度：0.5

  解析