2022-2023學年福建省漳州三中高二（下）期中數學試卷

一、單項選擇題：本大題共8小題，每小題5分，共40分，在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知函數f（x）=x²-x,則f（x）從2到2+Δx的平均變化率為（　　）

  A．2	B．Δx+3
  C．（Δx）2+3Δx	D．（Δx）2+3Δx+2
  組卷：34引用：3難度：0.7

  解析

• 2．過點P（0，2）作曲線y=

  1

  x

  的切線，則切點坐標為（　　）

  A．（1，1）

  B．（2， 1 2 ）

  C．（3， 1 3 ）

  D．（0，1）
  組卷：299引用：4難度：0.7

  解析

• 3．已知直線l₁的方向向量

  a

  =（2，4，x），直線l₂的方向向量

  b

  =（2，y,2），若|

  a

  |=6，且

  a

  ⊥

  b

  ，則x+y的值是（　　）

  A．-3或1

  B．3或-1

  C．-3

  D．1
  組卷：206引用：24難度：0.9

  解析

• 4．某班組織由甲，乙，丙等5名同學參加的演講比賽，現采用抽簽法決定演講順序，在“學生甲不是第一個出場，學生乙不是最后一個出場”的前提下，學生丙第一個出場的概率為（　　）

  A． 3 13

  B． 4 13

  C． 1 4

  D． 1 5
  組卷：2449引用：9難度：0.4

  解析

• 5．我們把分子、分母同時趨近于0的分式結構稱為

  0

  0

  型，比如：當x→0時，

  e

  x

  -

  1

  x

  的極限即為

  0

  0

  型．兩個無窮小之比的極限可能存在，也可能不存在，為此，洛必達在1696年提出洛必達法則：在一定條件下通過對分子、分母分別求導再求極限來確定未定式值的方法．如

  x

  →

  0

  lim

  e

  x

  -

  1

  x

  =

  x

  →

  0

  lim

  （

  e

  x

  -

  1

  ）

  ′

  x

  ′

  =

  x

  →

  0

  lim

  e

  x

  1

  =

  x

  →

  0

  lim

  e^x=e⁰=1，則

  x

  →

  1

  lim

  x

  2

  lnx

  x

  2

  -

  1

  =（　　）

  A．0

  B． 1 2

  C．1

  D．2
  組卷：105引用：6難度：0.8

  解析

• 6．已知函數f（x）=

  1

  2

  x

  2

  -ax+lnx-2有兩個極值點，則a的取值范圍是（　　）

  A．{a|a＜-2或a＞2}

  B．{a|a＜-2}

  C．{a|a＞2}

  D．{a|a≤-2或a≥2}
  組卷：62引用：1難度：0.6

  解析

• 7．海口鐘樓的歷史悠久，最早是為適應對外通商而建立，已成為海口的最重要的標志性與象征性建筑物之一．如圖所示，海口鐘樓的主體結構可以看作一個長方體，四個側面各有一個大鐘，則從8：00到10：00這段時間內，相鄰兩面鐘的分針所成角為60°的次數為（　　）

  A．2

  B．4

  C．6

  D．8
  組卷：35引用：2難度：0.6

  解析

四、解答題：本大題共6小題，共70分，解答應寫出文字說明、證明過程或演算步驟。

• 21．如圖（1），菱形ABCD中，∠ABC=120°，動點E，F分別在邊AD，AB上（不含端點），且

  EF

  =

  λ

  DB

  （0＜λ＜1），沿EF將△AEF向上折起得到△PEF，使得平面PEF⊥平面BCDEF，如圖（2）所示．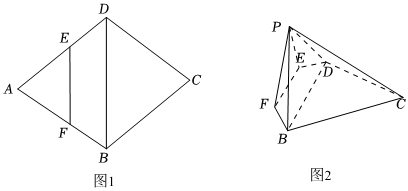
  
  （1）當λ為何值時，BF⊥PD；
  （2）若直線PC與平面BCDEF所成角的正切值為

  1

  3

  ，求平面PEF和平面PBD夾角的大小．
  組卷：181引用：4難度：0.5

  解析

• 22．已知函數f（x）=e^x-x+e³a,其中-

  6

  5

  ≤

  a

  ＜

  3

  e

  3

  -1，函數f（x）在（0，+∞）上的零點為x₀，函數g（x）=

  x + a - x - a e x ， 0 ≤ x ≤ x 0

  （ 1 - x ） lnx - a （ x + 1 ） ， x ＞ x 0

  ．
  （1）證明：
  ①3＜x₀＜4；
  ②函數g（x）有兩個零點；
  （2）設g（x）的兩個零點為x₁，x₂（x₁＜x₂），證明：

  e

  x

  2

  -

  x

  2

  e

  x

  1

  -

  x

  1

  ＞

  e

  x

  1

  +

  x

  2

  2

  ．
  （參考數據：e≈2.72，e²≈7.39，e³≈20.09，ln2≈0.69，ln3≈1.1）
  組卷：108引用：3難度：0.3

  解析