2023-2024學年山西省太原三十六中九年級（上）月考數學試卷（10月份）
發布：2024/9/7 4:0:8
一、選擇題（本大題共10小題，每小題3分，共30分。在每小題的四個選項中，只有一項最符合題意，請選出并在答題卡上將該項涂黑。）
-
1．下列方程中，屬于一元二次方程的是（ ）
組卷：2015引用：38難度：0.8 -
2．一元二次方程x2-8x-1=0配方后可變形為（ ）
組卷：1352引用：251難度：0.7 -
3．方程x2=5x的解是（ ）
組卷：733引用：12難度：0.7 -
4．用求根公式解一元二次方程3x2-2=4x時a,b,c的值是（ ）
組卷：799引用：5難度：0.7 -
5．如圖，在Rt△ABC中，∠ACB=90°，D是AB的中點，AB=8，則CD的長為（ ）組卷：287引用：3難度：0.6 -
6．如圖，兩張等寬的紙條交叉疊放在一起，重合部分構成四邊形ABCD．測得A，B的距離為6，A，C的距離為4，則B，D的距離是（ ）組卷：715引用：4難度：0.5 -
7．電影《滿江紅》于2023年1月22日在中國大陸上映，某地第一天票房約2億元，以后每天票房按相同的增長率增長，三天后票房收入累計達7億元，若把增長率記作x,則方程可以列為（ ）
組卷：356引用：8難度：0.6
三、解答題（本大題共8小題，75分。解答題應寫出文字說明、證明過程或演算步驟。）
-
22．小明在學習矩形這一節時知道“直角三角形斜邊上的中線等于斜邊的一半”，由此引發他的思考，這個定理的逆命題成立嗎？猜想：“如果一個三角形一邊上的中線等于這條邊的一半，那么這個三角形為直角三角形”．
通過探究，小明發現這個猜想也成立，以下是小明的證明過程：
已知：如圖1，在△ABC中，D是AB邊的中點，連接CD，且CD=AB．12
求證：△ABC為直角三角形．
證明：由條件可知，AD=BD=CD，則∠A=∠DCA，∠B=∠DCB．
又∵∠A+∠DCA+∠B+∠DCB=180°，
∴∠DCA+∠DCB=∠ACB=90°，即△ABC為直角三角形．
愛動腦筋的小明發現用本學期所學知識也能證明這個結論，并想出了圖2，圖3兩種不同的證明思路，請你選擇其中一種，把證明過程補充完整：證法一：如圖2，延長CD至點E，使DE=CD，連接AE，BE． 證法二：如圖3，分別取AC，BC邊的中點E，F，連接DE，DF，EF，則DE，DF，EF為△ABC的中位線． 組卷：206引用：2難度：0.6 -
23．探究問題：
（1）方法感悟：
如圖1，在正方形ABCD中，點E、F分別為DC、BC邊上的點，且滿足∠EAF=45°，連接EF，求證：DE+BF=EF．
感悟解題方法，并完成下列填空：
將△ADE繞點A順時針旋轉90°得到△ABG，此時AD與AB重合，由旋轉可得：
AB=AD，BG=DE，∠1=∠2，∠ABG=∠D=90°，
∴∠ABG+∠ABF=90°+90°=180°，
因此，點G、B、F在同一條直線上．
∵∠EAF=45°，
∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°．
∵∠1=∠2，∴∠1+∠3=45°．
即∠GAF=∠．
又 AG=AE，AF=AF，∴△GAF≌．
∴=EF，故DE+BF=EF；
（2）方法遷移：
如圖2，將Rt△ABC沿斜邊翻折得到△ADC，點E、F分別為DC、BC邊上的點，且∠EAF=∠DAB．試猜想DE、BF、EF之間有何數量關系，并證明你的猜想；12
（3）問題拓展：
如圖3，在四邊形ABCD中，AB=AD，E、F分別為DC、BC上的點，滿足∠EAF=∠DAB，試猜想當∠B與∠D滿足什么關系時，可使得DE+BF=EF．請直接寫出你的猜想（不必說明理由）．12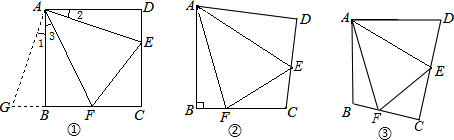
組卷：508引用：7難度：0.1