2022-2023學年陜西省寶雞市渭濱區八年級（下）期末數學試卷

一、選擇題（共8小題，每小題3分，過24分，每小題只有一個選項是符合題意的）

• 1．下列圖形中，既是軸對稱圖形又是中心對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：87引用：2難度：0.8

  解析

• 2．下列等式不成立的是（　　）

  A． a b = ac bc （c≠0）	B． am bm = a b （m≠0）
  C． a b = a c 2 b c 2	D． a b = a （ c 2 + 1 ） b （ c 2 + 1 ）
  組卷：1211引用：6難度：0.7

  解析

• 3．下列從左邊到右邊的變形，屬于因式分解的是（　　）

  A．（x+1）（x-1）=x2-1	B．x2-2x+1=x（x-2）+1
  C．x2-4y2=（x-2y）2	D．x2+2x+1=（x+1）2
  組卷：1138引用：6難度：0.7

  解析

• 4．如圖，在△ABC中，∠ABC=90°，AB=4，BC=3，若DE是△ABC的中位線，延長DE，交△ABC的外角∠ACM的平分線于點F，則線段DF的長為（　　）

  A．4

  B． 7 2

  C． 9 2

  D．5
  組卷：1077引用：7難度：0.5

  解析

• 5．已知關于x的不等式組

  x - a ≥ 0

  3 - 2 x ＞ 0

  的整數解共有4個，則a的取值范圍是（　　）

  A．-3≤a＜-2

  B．-3＜a≤-2

  C．-3＜a＜-2

  D．a＜-2
  組卷：3498引用：13難度：0.6

  解析

• 6．如圖，在△ABC中，∠ACB=90°，將△ABC繞點A順時針旋轉90°，得到△ADE，連接BD，若

  AC

  =

  4

  2

  ，DE=2，則線段BD的長為（　　）

  A．6

  B． 6 2

  C． 4 10

  D． 4 7
  組卷：464引用：7難度：0.7

  解析

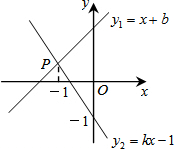• 7．如圖，直線y₁=x+b與y₂=kx-1相交于點P，若點P的橫坐標為-1，則關于x的不等式x+b＞kx-1的解集是（　　）

  A．x≥-1

  B．x＞-1

  C．x≤-1

  D．x＜-1
  組卷：8162引用：31難度：0.7

  解析

• 8．如圖在平行四邊形ABCD中，BE平分∠ABC，CF⊥BE，連接AE，G是AB的中點，連接GF，若AE=4，則GF=（　　）
  ?

  A．5

  B．4

  C．2

  D．3
  組卷：292引用：1難度：0.5

  解析

三、解答題（共13小題，計81分，解答應寫出過程）

• 25．上數學課時，王老師在講完乘法公式（a±b）²=a²±2ab+b²的多種運用后，要求同學們運用所學知識解答：求代數式x²+4x+5的最小值？同學們經過交流、討論，最后總結出如下解答方法：
  解：x²+4x+5=x²+4x+4+1=（x+2）²+1
  ∵（x+2）²≥0，
  ∴當x=-2時，（x+2）²的值最小，最小值是0，
  ∴（x+2）²+1≥1
  ∴當（x+2）²=0時，（x+2）²的值最小，最小值是1，
  ∴x²+4x+5的最小值是1．
  請你根據上述方法，解答下列各題
  （1）知識再現：當x=

  時，代數式x²-6x+12的最小值是

  ；
  （2）知識運用：若y=-x²+2x-3，當x=

  時，y有最

  值（填“大”或“小”），這個值是

  ；
  （3）知識拓展：若-x²+3x+y+5=0，求y+x的最小值．
  組卷：460引用：6難度：0.6

  解析

• 26．[問題初探]
  （1）如圖1，點E，F分別在正方形ABCD的邊BC，CD上，∠EAF=45°，試判斷EF、BE、DF之間的數量關系，聰明的小明是這樣做的：把△ABE繞點A逆時針旋轉90°至△ADG，使得AB與AD重合，由∠ADG=∠B=90°，得∠FDG=180°，即點F、D、G共線，易證△AFG≌

  ，故EF、BE、DF之間的數量關系為

  ．
  [類比探究]
  （2）如圖2，點E、F分別在正方形ABCD的邊CB、DC的延長線上，∠EAF=45°，連接EF，根據小明的發現容易探究得出EF、BE、DF之間的數量關系，探究思路及結果如下：
  在DC上截取DH=BE，連接AH，易證△ABE≌

  ，∴AE=AH，∠BAE=∠DAH，可以證明∴△EAF≌

  ，∴EF=

  ，∵FD=FH+DH，∴EF、BE、DF之間的數量關系為DF=

  ．
  [聯想拓展]
  （3）如圖3，在△ABC中，∠BAC=90°，AB=AC=3

  2

  ．點E、F均在邊BC上，且∠EAF=45°，若BE=2，求CF的長．
  
  組卷：393引用：2難度：0.3

  解析