2022-2023學年天津市八校聯考高三（上）期中數學試卷

一．選擇題（每題5分，共45分）

• 1．已知全集U={-1，0，1，2，3}，集合A={0，1，2}，B={-1，0，1}，則（?_UA）∩B=（　　）

  A．{-1}

  B．{0，1}

  C．{-1，2，3}

  D．{-1，0，1，3}
  組卷：705引用：24難度：0.9

  解析

• 2．設x∈R，則“|x-

  1

  2

  |＜

  1

  2

  ”是“x³＜1”的（　　）

  A．充分而不必要條件	B．必要而不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：4489引用：32難度：0.9

  解析

• 3．命題“?x∈[0，+∞），x³+x≥0”的否定是（　　）

  A．?x∈（-∞，0），x3+x＜0	B．?x∈（-∞，0），x3+x≥0
  C．?x0∈[0，+∞）， x 3 0 +x0＜0	D．?x0∈[0，+∞）， x 3 0 +x0≥0
  組卷：2094引用：77難度：0.9

  解析

• 4．函數

  f

  （

  x

  ）

  =

  x

  3

  +

  sinx

  e

  x

  +

  e

  -

  x

  的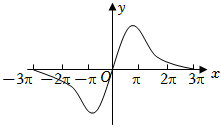圖象大致是（　　）

  A．	B．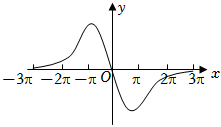
  C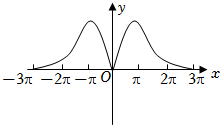．	D．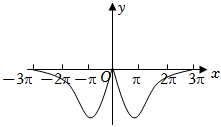
  組卷：244引用：8難度：0.8

  解析

• 5．已知等比數列{a_n}滿足a₁=2，

  a

  3

  ?

  a

  5

  =

  4

  a

  2

  6

  ，則a₃的值為（　　）

  A． 1 4

  B． 1 2

  C．1

  D．2
  組卷：513引用：5難度：0.8

  解析

• 6．設

  a

  =

  lo

  g

  1

  3

  2

  ，

  b

  =

  lo

  g

  1

  2

  1

  3

  ，

  c

  =

  （

  1

  2

  ）

  0

  .

  3

  ，則a,b,c大小關系為（　　）

  A．a＜c＜b

  B．a＜b＜c

  C．b＜a＜c

  D．b＜c＜a
  組卷：120引用：15難度：0.9

  解析

三、解答題（共75分）

• 19．已知等差數列{a_n}前n項和為S_n（n∈N₊），數列{b_n}是等比數列，a₁=3，b₁=1，b₂+S₂=10，a₅-2b₂=a₃．
  （1）求數列{a_n}和{b_n}的通項公式；
  （2）若

  c

  n

  =

  2 S n ， n 為奇數

  2 a n b n ， n 為偶數

  ，設數列{c_n}的前n項和為T_n，求T_2n．
  組卷：475引用：14難度：0.5

  解析

• 20．已知函數f（x）=-2a²lnx+

  1

  2

  x

  2

  +ax（a∈R）．
  （Ⅰ）當a=1時，求曲線y=f（x）在點（1，f（1））的切線方程；
  （Ⅱ）討論函數f（x）的單調性．
  組卷：89引用：6難度：0.5

  解析