當前位置：試卷中心 > 試卷詳情

2023-2024學年安徽省A10聯盟高二（上）開學摸底數學試卷（9月份）

發布：2024/8/12 5:0:1

一、選擇題（本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．）

1．已知復數z滿足z（2-i）=5，則|z|=（　　）
A．
5
2
B．
10
2
C．5 D．
5
組卷：27引用：3難度：0.9
解析
2．已知集合A={y|y=|cosx|，x∈R}，B={x|1-x²＜0}，則A∪（?_RB）=（　　）
A．[0，1] B．[-1，1] C．[-1，+∞） D．[1，+∞）
組卷：21引用：2難度：0.5
解析
3．“幸福感指數”是指某個人主觀地評價他對自己目前生活狀態滿意程度的指標，常用區間[0，10]內的一個數來表示，該數越接近10表示幸福感指數越高．已知甲、乙、丙、丁4人的幸福感指數分別為
lo
g
2
150
，
（
1
2
）
-
3
，
4
tan
（
-
300
°
）
，
（
5
）
ln
6
，則這4人的幸福感指數最高的是（　　）
A．甲 B．乙 C．丙 D．丁
組卷：29引用：2難度：0.7
解析
4．若向量
a
=
（
2
，-
1
）
，
b
=
（
3
，
4
）
，則
b
在
a
上的投影向量為（　　）
A．
（
4
5
，-
2
5
）
B．
（
4
5
5
，-
2
5
5
）
C．
（
6
5
，
8
5
）
D．
（
4
25
，-
2
25
）
組卷：36引用：2難度：0.7
解析
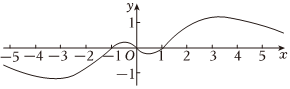5．已知函數f（x）的部分圖象如圖所示，則f（x）的解析式可能為（　　）
A．f（x）=x³?ln|x| B．f（x）=e^|x|?（x²-1）
C．
f
（
x
）
=
x
3
-
x
e
|
x
|
D．
f
（
x
）
=
x
-
x
3
2
x
組卷：45引用：4難度：0.7
解析
6．已知頂角為36°的等腰三角形為黃金三角形，底邊與腰長的比值為黃金分割比
5
-
1
2
，根據上述信息，可得sin126°=（　　）
A．
1
+
5
4
B．
5
+
5
8
C．
5
-
5
8
D．
3
-
5
8
組卷：103引用：2難度：0.7
解析
7．某校積極開展“戲曲進校園”活動，為了解該校各班參加戲曲興趣小組的人數，從全校隨機抽取5個班級，把每個班級參加該小組的人數作為樣本數據．已知樣本平均數為7，樣本標準差為2，且樣本數據互不相等，則該樣本數據的極差為（　　）
A．3 B．4 C．5 D．6
組卷：20引用：2難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題（本題共6小題，共70分，解答應寫出文字說明、證明過程或演算步驟）

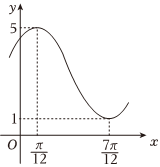21．已知函數
f
（
x
）
=
A
sin
（
ωx
+
φ
）
+
B
（
A
＞
0
，
ω
＞
0
，
|
φ
|
＜
π
2
）
的部分圖象如圖所示．
（1）求f（x）的解析式；
（2）將f（x）圖象上每個點的橫坐標變為原來的2倍（縱坐標不變），得到函數g（x）的圖象，若g（x）與h（x）的圖象關于
x
=
π
12
對稱，求不等式
h
（
sinx
）
≥
h
（
2
2
）
的解集．
組卷：54引用：2難度：0.4
解析
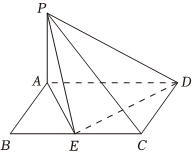22．如圖，PA⊥平面ABCD，四邊形ABCD為矩形，且AD=2AB=2PA=2，E為BC的中點．
（1）求直線PE與平面PAD所成角的正弦值；
（2）求二面角P-DE-A的正切值；
（3）探究在PA上是否存在點F，使得EF∥平面PCD，并說明理由．
組卷：62引用：3難度：0.5
解析