2022年寧夏石嘴山一中高考數(shù)學(xué)三模試卷（理科）

一、選擇題：本題共12小題，每小題5分，共60分．在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的．

• 1．設(shè)集合A={（x,y）|y=|x|}，B={（x,y）|x²+y²=1}，則A∩B的真子集的個(gè)數(shù)是（　　）

  A．2

  B．3

  C．4

  D．5
  組卷：81引用：2難度：0.7

  解析

• 2．已知角θ的終邊上有一點(diǎn)P（-4a,3a）（a＞0），則2sinθ+cosθ的值是（　　）

  A． - 2 5

  B． 2 5

  C． 2 5 或 - 2 5

  D．不確定
  組卷：215引用：1難度：0.8

  解析

• 3．一個(gè)家庭有兩個(gè)小孩，假設(shè)生男生女是等可能的，已知這個(gè)家庭有一個(gè)是女孩的條件下，這時(shí)另一個(gè)也是女孩的概率是（　　）

  A． 1 4

  B． 2 3

  C． 1 2

  D． 1 3
  組卷：572引用：6難度：0.9

  解析

• 4．費(fèi)馬數(shù)是以法國(guó)數(shù)學(xué)家費(fèi)馬命名的一組自然數(shù)，具有形式為

  2

  2

  n

  +

  1

  （

  記做F_n），其中n為非負(fù)數(shù)．費(fèi)馬對(duì)n=0，1，2，3，4的情形做了檢驗(yàn)，發(fā)現(xiàn)這組費(fèi)馬公式得到的數(shù)都是素?cái)?shù)，便提出猜想：費(fèi)馬數(shù)是質(zhì)數(shù)．直到1732年，數(shù)學(xué)家歐拉發(fā)現(xiàn)

  F

  5

  =

  2

  2

  5

  +

  1

  為合數(shù)，宣布費(fèi)馬猜想不成立．?dāng)?shù)列{a_n}滿(mǎn)足a_n=log₂（F_n-1），則數(shù)列{a_n}的前n項(xiàng)和S_n滿(mǎn)足S_n＞2020的最小自然數(shù)是（　　）

  A．9

  B．10

  C．11

  D．12
  組卷：34引用：1難度：0.6

  解析

• 5．雙曲線(xiàn)E與橢圓

  C

  ：

  x

  2

  6

  +

  y

  2

  2

  =

  1

  焦點(diǎn)相同且離心率是橢圓C離心率的

  3

  倍，則雙曲線(xiàn)E的標(biāo)準(zhǔn)方程為（　　）

  A． x 2 - y 2 3 = 1

  B．y2-2x2=1

  C． x 2 2 - y 2 2 = 1

  D． x 2 3 - y 2 = 1
  組卷：115引用：3難度：0.7

  解析

• 6．已知函數(shù)y=f（x）為R上的偶函數(shù)，若對(duì)于x≥0時(shí)，都有f（x）=f（x+4），且當(dāng)x∈[0，2）時(shí)，f（x）=log₂（x+1），則f（-2021）等于（　　）

  A．1

  B．-1

  C．log26

  D． lo g 2 3 2
  組卷：247引用：2難度：0.8

  解析

• 7．如圖，網(wǎng)格紙上小正方形的邊長(zhǎng)為1，粗實(shí)線(xiàn)畫(huà)出的是某多面體的三視圖，則該多面體的表面積為（　　）
  

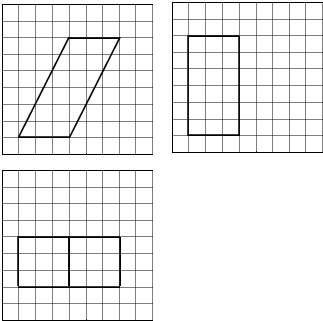
  A．18+36 5

  B．54+18 5

  C．90

  D．81
  組卷：4488引用：18難度：0.9

  解析

（二）選考題：共10分。請(qǐng)考生在22、23題中任選一題作答．如果多做，按所作第一題計(jì)分．[選修4-4：坐標(biāo)系與參數(shù)方程]

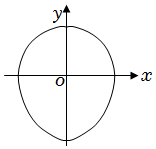• 22．如圖，某“京劇臉譜”的輪廓曲線(xiàn)C由曲線(xiàn)C₁和C₂圍成．在平面直角坐標(biāo)系xOy中，C₁的參數(shù)方程為

  x = 3 cost

  y = 3 sint

  （t為參數(shù)，且0≤t≤π），以坐標(biāo)原點(diǎn)為極點(diǎn)，x軸正半軸為極軸建立極坐標(biāo)系，C₂的極坐標(biāo)方程為ρ²=

  144

  9

  +

  7

  cos

  2

  θ

  （π≤θ≤2π）．
  （1）求C₁的普通方程和C₂的直角坐標(biāo)方程；
  （2）已知曲線(xiàn)C₁與x軸、y軸的正半軸分別交于A、B兩點(diǎn)，求曲線(xiàn)C₂上任意一點(diǎn)到直線(xiàn)AB的距離的最大值．
  組卷：77引用：1難度：0.5

  解析

[選修4-5：不等式選講]

• 23．已知函數(shù)f（x）=

  |

  1

  2

  x

  |

  -

  |

  1

  2

  x

  -

  m

  |

  的最大值為4．
  （Ⅰ）求實(shí)數(shù)m的值；
  （Ⅱ）若m＞0，0＜x＜

  m

  2

  ，求

  2

  |

  x

  |

  +

  2

  |

  x

  -

  2

  |

  的最小值．
  組卷：94引用：10難度：0.6

  解析