2022-2023學年廣東省湛江市雷州市八年級（上）期末數學試卷

一、選擇題（本大題共10小題，每小題3分，共30分）

• 1．下列圖案屬于軸對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：274引用：38難度：0.9

  解析

• 2．下列各式中，最簡分式是（　　）

  A． abc b

  B． 6 x 8 y

  C． x + 2 x - 3

  D． x 2 - 1 x + 1
  組卷：420引用：5難度：0.7

  解析

• 3．四邊形的內角和為（　　）

  A．180°

  B．360°

  C．540°

  D．720°
  組卷：246引用：29難度：0.9

  解析

• 4．用科學記數法表示數0.000301正確的是（　　）

  A．3×10-4

  B．301×10-8

  C．3.01×10-4

  D．3.01×10-5
  組卷：73引用：2難度：0.9

  解析

• 5．下列計算正確的是（　　）

  A．a3+3a3=4a6

  B．（a3）2=a5

  C．a6÷a2=a3

  D．a3?a3=a6
  組卷：41引用：4難度：0.7

  解析

• 6．若等腰三角形的底角是頂角的2倍，則這個等腰三角形的底角的度數是（　　）

  A．36°

  B．72°

  C．36°或72°

  D．無法確定的
  組卷：859引用：6難度：0.9

  解析

• 7．如果分式

  x

  x

  +

  1

  有意義，那么x的取值范圍是（　　）

  A．x≠0

  B．x≠1

  C．x≠-1

  D．x≠0或x≠-1
  組卷：114引用：2難度：0.9

  解析

五、解答題（三）（本大題共2小題，每小題12分，共24分）

• 22．閱讀材料：我們知道，“整體思想”是中學數學解題中的一種重要的思想方法，它在多項式的化簡與求值中應用極為廣泛．如4a-2a+a=（4-2+1）a=3a,類似地，我們把（x+y）看成一個整體，則4（x+y）-2（x+y）+（x+y）=（4-2+1）（x+y）=3（x+y）．請仿照上面的解題方法，完成下列問題：
  【嘗試應用】
  （1）把（x-y）²看成一個整體，合并3（x-y）²-6（x-y）²+2（x-y）²=

  ；
  （2）已知a²-2b=4，求3a²-6b-21的值；
  【拓廣探索】
  （3）已知a-5b=3，5b-3c=-5，3c-d=10，求（a-3c）+（5b-d）-（5b-3c）的值．
  組卷：362引用：12難度：0.6

  解析

• 23．如圖①，在△ABC中，AB=AC，點P為邊BC上異于B和C的任意一點，過點P作PD⊥AB于D，作PE⊥AC于E，過點C作CF⊥AB于F，求證：PD+PE=CF．
  
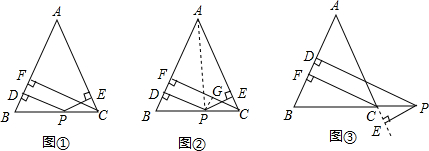
  （1）有下面兩種證明思路：（一）如圖②，連接AP，由△ABP于△ACP面積之和等于△ABC的面積證得PD+PE=CF．（二）如圖②，過點P作PG⊥CF，垂足為G，可以證明：PD=GF，PE=CG，則PD+PE=CF．
  請你選擇其中的一種證明思路完成證明：
  （2）探究：如圖③，當點P在BC的延長線上時，其它條件不變，探究并證明PD、PE和CF間的數量關系；
  （3）猜想：當點P在CB的延長線上時，其它條件不變，猜想PD、PE和CF間的數量關系（不要求證明）
  組卷：315引用：2難度：0.1

  解析