華師大新版九年級上冊《第22章 一元二次方程》2020年單元測試卷（5）

一、選擇題（本大題共9小題，共27分）

• 1．下列各方程中，一定是關(guān)于x的一元二次方程的是（　　）

  A．2x2+3=2x（5+x）	B．a(chǎn)x2+c=0
  C．（a+1）x2+6x+1=0	D．（a2+1）x2-3x+1=0
  組卷：152引用：4難度：0.9

  解析

• 2．已知方程x²+mx+3=0的一個根是1，則m的值為（　　）

  A．4

  B．-4

  C．3

  D．-3
  組卷：814引用：14難度：0.9

  解析

• 3．下列一元二次方程是一般形式的為（　　）

  A．（x-1）2=0

  B．3x2-4x+1=0

  C．x（x+5）=0

  D．（x+6）2-9=0
  組卷：382引用：2難度：0.9

  解析

• 4．x²-6x=1，左邊配成一個完全平方式得（　　）

  A．（x-3）2=10

  B．（x-3）2=9

  C．（x-6）2=8

  D．（x-6）2=10
  組卷：157引用：7難度：0.9

  解析

• 5．已知x=2是一元二次方程（m-2）x²+4x-m²=0的一個根，則m的值為（　　）

  A．0

  B．4

  C．0或4

  D．0或-4
  組卷：203引用：3難度：0.9

  解析

• 6．關(guān)于x的一元二次方程x²-2x+a=0有兩不等實根，則a的取值范圍是（　　）

  A．a(chǎn)＜1

  B．a(chǎn)≤1

  C．a(chǎn)＞1

  D．a(chǎn)≥1
  組卷：66引用：5難度：0.9

  解析

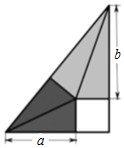• 7．我國古代偉大的數(shù)學(xué)家劉徽將勾股形（古人稱直角三角形為勾股形）分割成一個正方形和兩對全等的直角三角形．后人借助這種分割方法所得的圖形證明了勾股定理，如圖所示若a=3，b=4，則該三角形的面積為（　　）

  A．10

  B．12

  C． 99 8

  D． 53 4
  組卷：501引用：7難度：0.6

  解析

三、解答題（本大題共6小題，共55分）

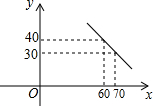• 20．某商店以30元/千克的單價新進(jìn)一批商品．經(jīng)調(diào)查發(fā)現(xiàn)，在一段時間內(nèi)，銷售量y（千克）與銷售單價x（元/千克）之間為一次函數(shù)關(guān)系，如圖所示．
  （1）求y與x的函數(shù)解析式；
  （2）要使利潤達(dá)到600元，銷售單價應(yīng)定為每千克多少元？
  組卷：356引用：4難度：0.7

  解析

• 21．閱讀材料：各類方程的解法
  求解一元一次方程，根據(jù)等式的基本性質(zhì)，把方程轉(zhuǎn)化為x=a的形式．求解二元一次方程組，把它轉(zhuǎn)化為一元一次方程來解；類似的，求解三元一次方程組，把它轉(zhuǎn)化為解二元一次方程組．求解一元二次方程，把它轉(zhuǎn)化為兩個一元一次方程來解．求解分式方程，把它轉(zhuǎn)化為整式方程來解，由于“去分母”可能產(chǎn)生增根，所以解分式方程必須檢驗．各類方程的解法不盡相同，但是它們有一個共同的基本數(shù)學(xué)思想--轉(zhuǎn)化，把未知轉(zhuǎn)化為已知．
  用“轉(zhuǎn)化”的數(shù)學(xué)思想，我們還可以解一些新的方程．例如，一元三次方程x³+x²-2x=0，可以通過因式分解把它轉(zhuǎn)化為x（x²+x-2）=0，解方程x=0和x²+x-2=0，可得方程x³+x²-2x=0的解．
  （1）問題：方程x³+x²-2x=0的解是x₁=0，x₂=

  ，x₃=

  ；
  （2）拓展：用“轉(zhuǎn)化”思想求方程

  2

  x

  +

  3

  =x的解；
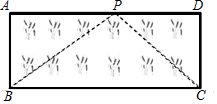
  （3）應(yīng)用：如圖，已知矩形草坪ABCD的長AD=8m,寬AB=3m,小華把一根長為10m的繩子的一端固定在點B，沿草坪邊沿BA，AD走到點P處，把長繩PB段拉直并固定在點P，然后沿草坪邊沿PD、DC走到點C處，把長繩剩下的一段拉直，長繩的另一端恰好落在點C．求AP的長．
  組卷：6053引用：40難度：0.1

  解析