2023年天津市十二區縣重點學校高考數學模擬試卷（一）

一、選擇題（本大題共9小題，共45分。在每小題列出的選項中，選出符合題目的一項）

• 1．設全集U={0，1，2，3，4}，集合A={x∈U||x-2|＜1}，則?_UA=（　　）

  A．{x|1＜x＜3}

  B．{x|1≤x≤3}

  C．{2}

  D．{0，1，3，4}
  組卷：418引用：8難度：0.7

  解析

• 2．已知平面α內一條直線l及平面β，則“l⊥β”是“α⊥β”的（　　）

  A．充分必要條件	B．充分不必要條件
  C．必要不充分條件	D．既不充分也不必要條件
  組卷：468引用：11難度：0.9

  解析

• 3．若

  a

  、

  b

  是兩個單位向量，其夾角是θ，則“

  π

  3

  ＜

  θ

  ＜

  π

  2

  ”是“

  |

  a

  -

  b

  |

  ＞

  1

  ”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：183引用：2難度：0.8

  解析

• 4．函數

  f

  （

  x

  ）

  =

  sinx

  1

  +

  cosx

  的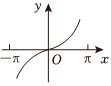部分圖象大致為（　　）

  A．

  B．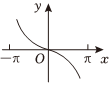

  C．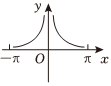

  D．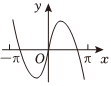
  組卷：338引用：7難度：0.9

  解析

• 5．某中學有高中生3000人，初中生2000人，高中生中男生、女生人數之比為3：7，初中生中男生、女生人數之比為6：4，為了解學生的學習狀況，用分層抽樣的方法從該校學生中抽取一個容量為N的樣本，已知從初中生中抽取男生12人，則從高中生中抽取的女生人數是（　　）

  A．12

  B．15

  C．20

  D．21
  組卷：317引用：5難度：0.8

  解析

• 6．已知函數f（x）=e^x+1，a=f（log₂0.2），b=f（2^0.2），c=f（0.2^0.3），則（　　）

  A．a＜b＜c

  B．a＜c＜b

  C．b＜a＜c

  D．b＜c＜a
  組卷：415引用：2難度：0.8

  解析

三、解答題（本大題共5小題，共75分。解答應寫出文字說明，證明過程或演算步驟）

• 19．設{a_n}是等差數列，{b_n}是等比數列．已知a₁=4，b₁=6，b₂=2a₂-2，b₃=2a₃+4．
  （Ⅰ）求{a_n}和{b_n}的通項公式；
  （Ⅱ）設數列{c_n}滿足

  c

  1

  =

  1

  ，

  c

  n

  =

  1 ， 2 k ＜ n ＜ 2 k + 1

  b k ， n = 2 k

  ，其中k∈N^*．
  （i）求數列

  {

  a

  2

  n

  （

  c

  2

  n

  -

  1

  ）

  }

  的通項公式；
  （ii）求

  n

  ∑

  i

  =

  1

  a

  2

  i

  c

  2

  i

  （

  n

  ∈

  N

  *

  ）

  ．
  組卷：543引用：1難度：0.3

  解析

• 20．已知函數f（x）=

  1

  2

  a

  x

  2

  -x-lnx（a∈R）．
  （1）討論f（x）的單調性；
  （2）當x≥1時，|f（x）|≥2，求a的取值范圍；
  （3）證明：

  n

  ∑

  k

  =

  2

  1

  lnk

  ＞

  1

  -

  1

  n

  ．
  組卷：871引用：8難度：0.2

  解析