2023-2024學年福建省寧德市壽寧一中高二（上）期初數學試卷

一、單選題（共40分）

• 1．已知復數z滿足（z+2i）（2-i）=5，則z的共軛復數

  z

  =（　　）

  A．2-i

  B．2+i

  C．-2+i

  D．-2-i
  組卷：120引用：7難度：0.8

  解析

• 2．如圖①，普通蒙古包可近似看作是圓柱和圓錐的組合體；如圖②，已知圓柱的底面直徑AB=16米，AD=4米，圓錐的高PQ=6米，則該蒙古包的側面積約為（　　）
  

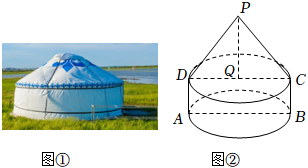
  A．336π平方米

  B．272π平方米

  C．208π平方米

  D．144π平方米
  組卷：117引用：7難度：0.7

  解析

• 3．設x₀為函數f（x）=lnx+x-5的零點，則不等式x-x₀＞2的最小整數解為（　　）

  A．3

  B．4

  C．6

  D．5
  組卷：26引用：2難度：0.7

  解析

• 4．某小區從2000戶居民中隨機抽取100戶進行月用電量調查，發現他們的用電量都在50～350kW?h之間，進行適當的分組后（每組為左閉右開的區間），畫出頻率分布直方圖如圖所示．則（　　）
  

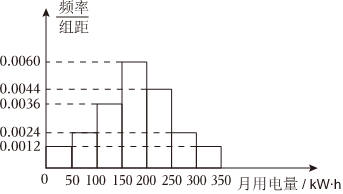
  A．小區用電量平均數為186.5，極差為300

  B．小區用電量中位數為171，眾數為175

  C．可以估計小區居民月用電量的85%分位數約為262.5

  D．小區用電量不小于250kW?h的約有380戶
  組卷：226引用：3難度：0.6

  解析

• 5．已知函數

  f

  （

  x

  ）

  =

  sin

  2

  x

  +

  3

  cos

  2

  x

  ，則下列說法錯誤的是（　　）

  A．函數f（x）的最小正周期為π

  B． x = 7 π 12 是函數f（x）的一條對稱軸

  C．函數f（x）在區間 [ - π 3 ， π 6 ] 上的最大值為2

  D．將函數f（x）向左平移 π 6 個單位后得函數g（x），則g（x）為偶函數
  組卷：96引用：4難度：0.6

  解析

• 6．函數

  f

  （

  x

  ）

  =

  7

  +

  2

  ax

  -

  x

  2

  在區間[-1，1]上單調遞減，則a的取值范圍為（　　）

  A．a≤-1

  B．a＜-1

  C．-3≤a≤-1

  D．-3＜a＜-1
  組卷：262引用：7難度：0.8

  解析

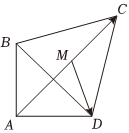• 7．如圖，在平面四邊形ABCD中，∠A=90°，AB=AD=2，△BCD為等邊三角形，當點M在對角線AC上運動時，

  MC

  ?

  MD

  的最小值為（　　）

  A．-2

  B． - 3 2

  C．-1

  D． - 1 2
  組卷：90引用：5難度：0.7

  解析

四、解答題（共70分）

• 21．已知函數f（x）=log_a（10+x）-log_a（10-x）（a＞0且a≠1）．
  （1）求f（x）的定義域；
  （2）判斷f（x）的奇偶性，并說明理由；
  （3）求不等式f（x）＞0的解集．
  組卷：226引用：4難度：0.7

  解析

• 22．如圖所示，在等邊△ABC中，AB=6，M，N分別是AB，AC上的點，且AM=AN=4，E是BC的中點，AE交MN于點F．以MN為折痕把△AMN折起，使點A到達點P的位置（0＜∠PFE＜π），連接PB，PE，PC．
  
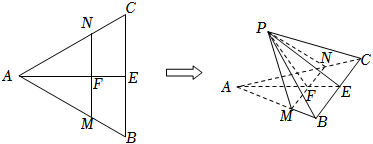
  （1）證明：MN⊥PE；
  （2）設點P在平面ABC內的射影為點Q，若二面角P-MN-B的大小為

  2

  3

  π

  ，求直線QC與平面PBC所成角的正弦值．
  組卷：170引用：4難度：0.6

  解析