2022-2023學年重慶市江北區巴川量子中學八年級（上）期末數學試卷

一、選擇題（本大題12個小題，每小題4分，共48分）在每個小題的下面，都給出了代號為A、B、C、D的四個答案，其中只有一個是正確的，請將答題卡上題號右側正確答案所對應的方框涂黑．

• 1．用數學的眼光觀察下面的網絡圖標，其中可以抽象成軸對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：336引用：22難度：0.8

  解析

• 2．“冠狀病毒”是一個大型病毒家族，科學家借助電子顯微鏡研究發現，某冠狀病毒的直徑約為0.00000012米，0.00000012用科學記數法表示為（　　）

  A．1.2×10-6

  B．1.2×10-7

  C．1.2×10-8

  D．1.2×10-9
  組卷：273引用：4難度：0.8

  解析

• 3．下列各式屬于最簡二次根式是（　　）

  A． 1 2

  B． 4

  C． 6

  D． 8
  組卷：97引用：7難度：0.9

  解析

• 4．下列長度的三條線段，能組成三角形的是（　　）

  A．3，4，7

  B．6，7，12

  C．6，7，14

  D．3，4，8
  組卷：1265引用：11難度：0.8

  解析

• 5．下列運算正確的是（　　）

  A．3a+a=4a2	B．（-2a）3=-8a3
  C．（a3）2÷a5=1	D．3a3?2a2=6a6
  組卷：692引用：14難度：0.8

  解析

• 6．若x²-mx+16能用完全平方公式進行因式分解，則m的值為（　　）

  A．-4

  B．8

  C．-4或4

  D．-8或8
  組卷：618引用：1難度：0.7

  解析

• 7．已知一個正多邊形的每一個外角都是30°，則這個正多邊形的邊數是（　　）

  A．12

  B．10

  C．9

  D．8
  組卷：197引用：1難度：0.9

  解析

• 8．下列結論正確的是（　　）

  A．兩個等邊三角形全等

  B．有一個銳角相等的兩個直角三角形全等

  C．有兩邊及一個角對應相等的兩個三角形全等

  D．斜邊和一個銳角對應相等的兩個直角三角形全等
  組卷：673引用：4難度：0.8

  解析

三、解答題：（本大題8個小題，其中19題8分，其余題目每小題8分，共78分）解答時每小題必須給出必要的演算過程或推理步驟，畫出必要的圖形（包括輔助線），請將解答過程書寫在答題卡中對應的位置上．

• 25．對于一個四位正整數，如果其十位數字等于千位數字減去百位數字，個位數字等于百位數字減去十位數字，則稱這個四位數為“山峰數”．對于一個“山峰數”A=

  abcd

  （a、b、c、d是整數且1≤a≤9，0≤b、c、d≤9），它的千位數字和百位數字組成的兩位數為

  ab

  ，十位數字和個位數字組成的兩位數為

  cd

  ，將這兩個兩位數求和記作t；它的千位數字和十位數字組成的兩位數為

  ac

  ，它的百位數字和個位數字組成的兩位數為

  bd

  ，將這兩個兩位數求和記作s,規定：F（A）=

  t

  -

  s

  9

  ．
  例如：A=3211，因為3-2=1，2-1=1，故3211是一個“山峰數”，
  t=32+11=43，s=31+21=52，則F（A）=

  t

  -

  s

  9

  =-1
  （1）判斷6514和9542是否是“山峰數”，如果是，求出相應的F（A）；
  （2）記最小的“山峰數”M的各個數位數字之和為m.若“山峰數”A滿足

  m

  |

  F

  （

  A

  ）

  |

  被3整除，并且A≠M．求所有滿足條件的“山峰數”A．
  組卷：157引用：1難度：0.4

  解析

• 26．已知△ABC是正三角形，D為BC邊上一點，連接AD．
  （1）如圖1，在AC上截取點E，使得CE=BD，連接BE交AD于點F，若FD=2，BE=8，求點A到BE的距離；
  （2）如圖2，在（1）的條件下，連接CF，取AB的中點G，連接FG，證明CF=2FG；
  （3）如圖3，點P為△ABC內部一點，連接AP，將線段AC繞點A逆時針旋轉得到線段AQ，∠CAQ=∠BAP．
  將△ABP沿AP翻折到同一平面內的△ATP，在線段AQ上截取AM=AP，連接MT．已知MT=6，PT=8，AM=10．直接寫出△AMT的面積．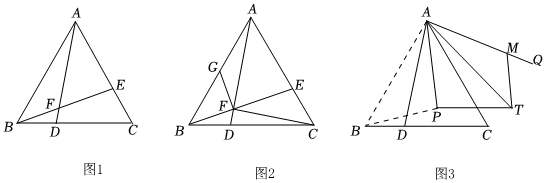
  
  組卷：296引用：1難度：0.1

  解析