2011年湖北省天門市八年級(jí)數(shù)學(xué)競(jìng)賽試卷

一、選擇題（每小題4分，共32分）

• 1．若a、b、c是三角形的三邊，則下列關(guān)系式中正確的是（　　）

  A．a(chǎn)2-b2-c2-2bc＞0	B．a(chǎn)2-b2-c2-2bc=0
  C．a(chǎn)2-b2-c2-2bc＜0	D．a(chǎn)2-b2-c2-2bc≤0
  組卷：213引用：4難度：0.9

  解析

• 2．定義一種運(yùn)算☆，其規(guī)則為a☆b=

  1

  a

  +

  1

  b

  ，根據(jù)這個(gè)規(guī)則2☆（x+1）=

  3

  2

  的解為（　　）

  A．x= - 2 3

  B． x = - 1 4

  C． x = - 1 3

  D．x=0
  組卷：134引用：2難度：0.9

  解析

• 3．若（1-2x+y）是4xy-4x²-y²-m的一個(gè)因式，則m的值為（　　）

  A．4

  B．1

  C．-1

  D．0
  組卷：972引用：17難度：0.9

  解析

• 4．設(shè)0＜k＜1，關(guān)于x的一次函數(shù)y=kx+

  1

  k

  （1-x），當(dāng)1≤x≤2時(shí)，y的最大值是（　　）

  A．k

  B． 2 k - 1 k

  C． 1 k

  D． k + 1 k
  組卷：1049引用：17難度：0.7

  解析

• 5．已知a、b、c為三個(gè)正整數(shù)，如果a+b+c=12，那么以a、b、c為邊能組成的三角形可能是：①等腰三角形；②等邊三角形；③直角三角形；④鈍角三角形．以上符合條件的正確結(jié)論個(gè)數(shù)為（　　）

  A．1個(gè)

  B．2個(gè)

  C．3個(gè)

  D．4個(gè)
  組卷：92引用：1難度：0.9

  解析

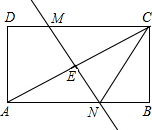• 6．如圖，長(zhǎng)方形ABCD中，AB=4，BC=3，將其沿直線MN折疊，使點(diǎn)C與點(diǎn)A重合，則CN的長(zhǎng)為（　　）

  A． 7 2

  B． 25 8

  C． 27 8

  D． 15 4
  組卷：1661引用：27難度：0.7

  解析

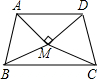• 7．如圖，△ABM與△CDM是兩個(gè)全等的等邊三角形，MA⊥MD．有下列四個(gè)結(jié)論：（1）∠MBC=25°；（2）∠ADC+∠ABC=180°；（3）直線MB垂直平分線段CD；（4）四邊形ABCD是軸對(duì)稱圖形．其中正確結(jié)論的個(gè)數(shù)為（　　）

  A．1個(gè)

  B．2個(gè)

  C．3個(gè)

  D．4
  組卷：327引用：10難度：0.7

  解析

三、解答題（共56分）

• 21．（1）如圖1，在正方形ABCD中，M是BC邊（不含端點(diǎn)B、C）上任意一點(diǎn)，P是BC延長(zhǎng)線上一點(diǎn)，N是∠DCP的平分線上一點(diǎn)．若∠AMN=90°，求證：AM=MN．
  下面給出一種證明的思路，你可以按這一思路證明，也可以選擇另外的方法證明．
  證明：在邊AB上截取AE=MC，連ME．
  正方形ABCD中，∠B=∠BCD=90°，AB=BC．
  ∴∠NMC=180°-∠AMN-∠AMB=180°-∠B-∠AMB=∠MAB=∠MAE．
  （下面請(qǐng)你完成余下的證明過程）
  （2）若將（1）中的“正方形ABCD”改為“正三角形ABC”（如圖2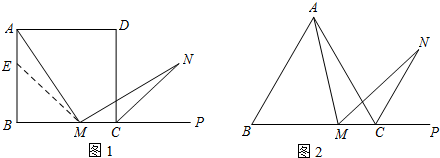），N是∠ACP的平分線上一點(diǎn)，則當(dāng)∠AMN=60°時(shí)，結(jié)論AM=MN是否還成立？請(qǐng)說明理由．
  組卷：217引用：5難度：0.5

  解析

• 22．如圖，雙曲線y=

  k

  x

  （k＞0，x＞0）的圖象上有兩點(diǎn)P₁（x₁，y₁）和P₂（x₂，y₂），且x₁＜x₂，分別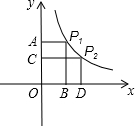過P₁和P₂向x軸作垂線，垂足為B、D．過P₁和P₂向y軸作垂線，垂足為A、C．
  （1）若記四邊形AP₁BO和四邊形CP₂DO的面積分別為S₁和S₂，周長(zhǎng)為C₁和C₂，試比較S₁和S₂，C₁和C₂的大小；
  （2）若P是雙曲線y=

  k

  x

  （k＞0，x＞0）的圖象上一點(diǎn)，分別過P向x軸、y軸作垂線，垂足為M、N．試問當(dāng)P點(diǎn)落在何處時(shí)，四邊形PMON的周長(zhǎng)最小？
  組卷：960引用：2難度：0.1

  解析