當前位置：試卷中心 > 試卷詳情

2021-2022學年北京市海淀區師達中學七年級（下）月考數學試卷（5月份）

發布：2024/4/20 14:35:0

一．選擇題（共10小題，滿分20分，每小題2分）

1．在實數，
5
，0，
6
7
，π，
3
16
，
9
中，無理數一共有（　　）
A．1個 B．2個 C．3個 D．4個
組卷：189引用：3難度：0.7
解析
2．下列圖形中，∠1和∠2為同旁內角的是（　　）
A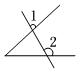． B． C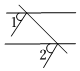． D．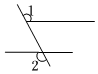
組卷：731引用：7難度：0.7
解析
3．在平面直角坐標系中，點B（2，3）到x軸的距離為（　　）
A．3 B．2 C．-3 D．-2
組卷：141引用：5難度：0.7
解析

4．下列調查中，適宜采用抽樣調查的是（　　）

A．調查某班學生的身高情況

B．調查亞運會100m游泳決賽運動員興奮劑的使用情況

C．調查某批汽車的抗撞擊能力

D．調查一架“殲10”隱形戰斗機各零部件的質量

組卷：220引用：8難度：0.8

解析

5．若a＞b,則下列各式不成立的是（　　）
A．2a＞a+b B．3-a＜3-b C．a²＞b² D．a-b＞0
組卷：180引用：5難度：0.6
解析
6．一個邊長為a的正方形的面積與一個長為6，寬為5的長方形的面積相等，則a的值（　　）
A．在6與7之間 B．在5與6之間 C．在4與5之間 D．在3與4之間
組卷：164引用：5難度：0.7
解析
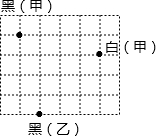7．如圖，圍棋棋盤放在某平面直角坐標系內，已知黑棋（甲）的坐標為（-2，2）黑棋（乙）的坐標為（-1，-2），則白棋（甲）的坐標是（　　）
A．（2，2） B．（0，1） C．（2，-1） D．（2，1）
組卷：8149引用：33難度：0.5
解析
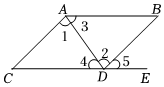8．如圖，點E在CD的延長線上，下列條件中能判定AC∥BD的是（　　）
A．∠CAB+∠C=180° B．∠2+∠B=180°
C．∠5=∠C D．∠3=∠4
組卷：296引用：8難度：0.6
解析
9．下列命題：
①內錯角相等；
②兩個銳角的和是鈍角；
③a,b,c是同一平面內的三條直線，若a∥b,b∥c,則a∥c；
④a,b,c是同一平面內的三條直線，若a⊥b,b⊥c,則a⊥c；
其中真命題的個數是（　　）
A．1個 B．2個 C．3個 D．4個
組卷：399引用：7難度：0.9
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三．解答題（共9小題，滿分48分，第19-20題每題8分，第21-26每題4分，第27-28題每題8分）

26．已知AB∥CD，點M、N分別在直線AB、CD上，∠AME與∠CNE的平分線所在的直線相交于點F．
（1）如圖1，點E、F都在直線AB、CD之間且∠MEN=70°時，∠MFN的度數為
；
（2）如圖2，當點E在直線AB、CD之間，F在直線CD下方時，寫出∠MEN與∠MFN之間的數量關系，并證明；
（3）如圖3，當點E在直線AB上方，F在直線AB與CD之間時，直接寫出∠MEN與∠MFN之間的數量關系．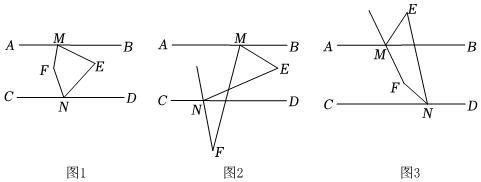
組卷：728引用：4難度：0.4
解析
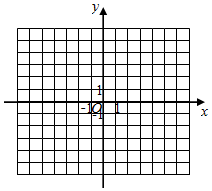27．在平面直角坐標系xOy中，橫、縱坐標都是整數的點叫做整點．給出如下定義：對于任意兩個整點M（x₁，y₁），N（x₂，y₂），M與N的“直角距離”記為d_MN，d_MN=|x₁-x₂|+|y₁-y₂|．
例如，點M（1，5）與N（7，2）的“直角距離”d_MN=|1-7|+|5-2|=9．
（1）已知點A（4，-1）．
①點A與點B（1，3）的“直角距離”d_AB=
；
②若點A與整點C（-2，m）的“直角距離”d_AC=8，則m的值為
；
（2）小明有一項設計某社區規劃圖的實踐作業，這個社區的道路都是正南正北，正東正西方向，并且平行的相鄰兩條路之間的距離都是相等的，可近似看作正方形的網格．小明建立平面直角坐標系畫出了此社區的示意圖（如圖所示）．為了做好社區消防，需要在某個整點處建一個消防站P，要求是：消防站與各個火警高危點的“直角距離”之和最小．目前該社區內有兩個火警高危點，分別是D（-2，-1）和E（2，2）．
①若對于火警高危點D和E，消防站P不僅要滿足上述條件，還需要消防站P到D，E兩個點的“直角距離”之差的絕對值最小，則滿足條件的消防站P的坐標可以是
（寫出一個即可），所有滿足條件的消防站P的位置共有
個；
②在設計過程中，如果社區還有一個火警高危點F（4，-2），那么滿足與這三個火警高危點的“直角距離”之和最小的消防站P的坐標為
．
組卷：740引用：5難度：0.6
解析