2022-2023學年陜西師大附中九年級（上）開學數學試卷

一、選擇題（共10小題，每小題3分，計30分.每小題只有一個選項是符合題意的）

• 1．下列方程中，①2x²+1=0；②ax²+bx+c=0；③2x-

  1

  x

  =0；④（x+2）（x-2）=x²-3，是一元二次方程的有（　　）

  A．1個

  B．2個

  C．3個

  D．4個
  組卷：1232引用：2難度：0.7

  解析

• 2．下列長度的各組線段中，成比例線段的是（　　）

  A．1cm,2cm,3cm,4cm	B．1cm,2cm,3cm,6cm
  C．2cm,4cm,6cm,8cm	D．3cm,4cm,5cm,10cm
  組卷：366引用：11難度：0.6

  解析

• 3．下面性質中矩形具有而菱形沒有的是（　　）

  A．對角線相等

  B．鄰邊相等

  C．對角線垂直

  D．對邊相等
  組卷：604引用：8難度：0.5

  解析

• 4．一元二次方程2x²-5x+1=0的根的情況是（　　）

  A．沒有實數根	B．有兩個相等的實數根
  C．有兩個不相等的實數根	D．無法確定
  組卷：1500引用：4難度：0.5

  解析

• 5．在育紅學校開展的課外閱讀活動中，學生人均閱讀量從七年級的每年100萬字增加到九年級的每年121萬字．設該校七至九年級人均閱讀量年均增長率為x,根據題意，所列方程正確的是（　　）

  A．100（1+x）2=121

  B．100×2（1+x）=121

  C．100（1+2x）=121

  D．100（1+x）+100（1+x）2=121
  組卷：1729引用：26難度：0.8

  解析

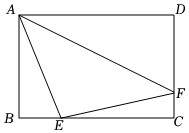• 6．如圖，矩形ABCD中，AB=2cm,BC=3cm,點E從點B出發，沿BC以2cm/s的速度向點C移動，同時點F從點C出發，沿CD以1cm/s的速度向點D移動，當E，F兩點中有一點到達終點時，另一點也停止運動．當△AEF是以AF為底邊的等腰三角形時，則點E運動時間為（　　）

  A． 6 + 31

  B． 6 - 31

  C．6

  D．6+ 31 或6- 31
  組卷：601引用：2難度：0.3

  解析

• 7．已知4是關于x的方程x²-（m+1）x+2m=0的一個實數根，并且這個方程的兩個實數根恰好是等腰△ABC的兩條邊的邊長，則△ABC的周長為（　　）

  A．7

  B．10

  C．11

  D．10或11
  組卷：232引用：5難度：0.7

  解析

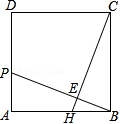• 8．如圖，在邊長為12的正方形ABCD中，點P在AD上，且不與A、D重合，點H在AB上，且不與A、B重合，連接BP、CH，BP與CH交于點E．若BP=CH且AP=5，則線段BE的長（　　）

  A．4

  B． 30 13

  C． 60 13

  D．5
  組卷：763引用：4難度：0.5

  解析

三、解答題（共8小題，共52分）

• 23．某商場將進貨價為30元的臺燈以40元售出，平均每月能售出600個，調查表明：售價在40～60元范圍內，這種臺燈的售價每上漲1元，其銷售量就將減少10個．為了實現平均每月10000元的銷售利潤，這種臺燈的售價應定為多少？這時應進臺燈多少個？
  組卷：3307引用：37難度：0.5

  解析

• 24．問題探究：
  將幾何圖形按照某種法則或規則變換成另一種幾何圖形過程叫做幾何變換．旋轉變換是幾何變換的一種基本模型．經過旋轉，往往能使圖形的幾何性質明白顯現，題設和結論中的元素由分散變為集中，相互之間的關系清楚明了，從而將求解問題靈活轉化．
  問題提出：
  如圖1，△ABC是邊長為1的等邊三角形，P為ABC內部一點，連接PA、PB、PC，求PA+PB+PC的最小值．
  問題解決：
  如圖2，將△BPA繞點B逆時針旋轉60°至△BP′A′，連接PP′、A′C，記A′C與AB交于點D，可知BA′=BA=BC=1，∠A′BC=∠A′BA+∠ABC=120°，由BP′=BP，∠P′BP=60°，可知△P′BP為等邊三角形，有PB=P′P．故PA+PB+PC=P′A′+P′P+PC≥A′C，因此，當A′、P′、P、C共線時，PA+PB+PC有最小值是

  ．
  學以致用：
  如圖3，P是邊長為3的正方形ABCD內一點，Q為邊BC上一點，連接PA、PD、PQ，求PA+PD+PQ的最小值．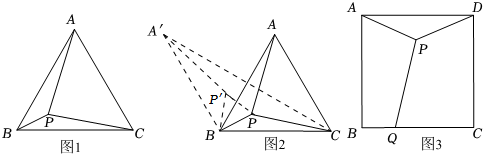
  
  組卷：582引用：1難度：0.4

  解析