2022-2023學年吉林省長春市南關區東北師大附中明珠校區八年級（上）期末數學試卷

一、選擇題（本大題共14道小題，每小題3分，共42分）

• 1．下列各數是無理數的是（　　）

  A． 1 3

  B．0

  C．-0.7

  D． 2
  組卷：82引用：3難度：0.9

  解析

• 2．若二次根式

  x

  -

  2

  在實數范圍內有意義，則x的取值范圍是（　　）

  A．x＞2

  B．x≥2

  C．x≤2

  D．x＜2
  組卷：854引用：17難度：0.9

  解析

• 3．下列計算正確的是（　　）

  A．3a2-a2=3

  B．a2?a3=a6

  C．（a2）3=a6

  D．a6÷a2=a3
  組卷：524引用：12難度：0.7

  解析

• 4．以下列各組數為邊長，能組成直角三角形的是（　　）

  A．2，3，4

  B． 2 ， 4 ， 7

  C．5，6，7

  D．5，12，13
  組卷：778引用：8難度：0.9

  解析

• 5．若n為整數，n＜

  13

  ＜n+1，則n的值為（　　）

  A．1

  B．0

  C．2

  D．3
  組卷：363引用：1難度：0.7

  解析

• 6．把多項式6a²b-3ab²+12a²b²分解因式，應提取的公因式是（　　）

  A．ab

  B．3ab2

  C．3ab

  D．12a2b2
  組卷：1341引用：7難度：0.7

  解析

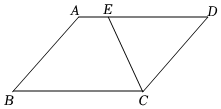• 7．如圖，在平行四邊形ABCD中，∠A=130°，CE平分∠BCD，則∠AEC的度數是（　　）

  A．115°

  B．110°

  C．105°

  D．120°
  組卷：255引用：2難度：0.5

  解析

二、解答題（本大題共9道小題，共78分）

• 22．【問題原型】如圖①，在△ABC中，點D是AB的中點，連結CD，CD=

  1

  2

  AB．求證：∠ACB=90°．
  請補全證明過程．
  證明：如圖①，∵點D是AB的中點（已知），
  ∴AD=BD=

  1

  2

  AB（中點定義）．
  ∵CD=

  1

  2

  AB（已知），
  ∴CD=AD=BD（等量代換）．
  ∴∠ACD=

  ，∠DCB=

  （

  ）．（填推理依據）
  ∵∠A+∠B+∠DCB+∠ACD=180°，
  ∴∠ACD+∠DCB=90°．
  ∴∠ACB=90°．
  【結論應用】如圖②，△ABC中，點D是AB的中點，連結CD，將△ACD沿CD翻折得到△A′CD，連結AA'，交CD于點O，連結A'B．請判斷A'B與CD的位置關系，并說明理由．
  【應用拓展】如圖③，在?ABCD中，∠A＜90°，點E是邊AB的中點，連結DE，將△ADE沿DE翻折得到△A′DE，連結BA'并延長，交CD于點F．若AB=5，AD=3，S_?ABCD=12，則BF的長為

  ．
  
  組卷：276引用：2難度：0.2

  解析

• 23．如圖，在?ABCD中，∠BAC=90°，CD=3cm,AC=4cm,動點P從點A出發沿AD以1cm/s速度向終點D運動，同時點Q從點C出發，以4cm/s速度沿射線CB運動，當點P到達終點時，點Q也隨之停止運動，設點P運動的時間為t秒（t＞0）．
  （1）CB的長為

  ．
  （2）用含t的代數式表示線段QB的長．
  （3）連接PQ，
  ①是否存在t的值，使得PQ與AC互相平分？若存在，求出t的值；若不存在，請說明理由；
  ②是否存在t的值，使得PQ與AB互相平分？若存在，求出t的值；若不存在，請說明理由．
  （4）若點P關于直線AQ對稱的點恰好落在直線AB上，請直接寫出t的值．
  
  組卷：299引用：1難度：0.2

  解析