2023年貴州省銅仁市碧江區(qū)中考數(shù)學(xué)模擬試卷（3月份）
發(fā)布：2024/5/11 8:0:9
一、選擇題：以下每小題均有A、B、C、D四個選項，其中只有一個選項正確，請用2B鉛筆在答題卡相應(yīng)位置作答，每小3分，共36分.
-
1．在-1，-2，0，
這四個數(shù)中，最小的數(shù)是（ ）9組卷：21引用：1難度：0.7 -
2．下列圖案中，既是軸對稱圖形又是中心對稱圖形的是（ ）
組卷：79引用：3難度：0.5 -
3．據(jù)統(tǒng)計，2023年銅仁市中考學(xué)生人數(shù)約5.8萬左右，用科學(xué)記數(shù)法表示“5.8萬”正確的是（ ）
組卷：8引用：2難度：0.8 -
4．下列說法正確的是（ ）
組卷：18引用：2難度：0.6 -
5．以方程組
的解為坐標(biāo)的點(diǎn)（x,y）在平面直角坐標(biāo)系中的位置是（ ）y=2x-5y=-x+1組卷：216引用：4難度：0.5 -
6．如圖是一個幾何體的三視圖，主視圖和左視圖均是面積為12的等腰三角形，俯視圖是直徑為6的圓，則這個幾何體的全面積是（ ）組卷：395引用：7難度：0.5 -
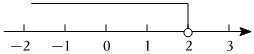7．一個不等式的解集在數(shù)軸上表示如圖，則這個不等式可以是（ ）組卷：176引用：8難度：0.7 -
8．將二次函數(shù)y=-（x-k）2+k+1的圖象向右平移1個單位，再向上平移2個單位后，頂點(diǎn)在直線y=2x+2上，則k的值為（ ）
組卷：183引用：1難度：0.5
三、解答題：本大題共9小題，共98分解答應(yīng)寫出必要的文字說明、證明過程或演算步驟.
-
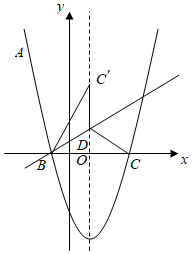24．如圖，拋物線y=ax2+bx+c經(jīng)過點(diǎn)A（-2，5），與x軸相交于B（-1，0），C（3，0）兩點(diǎn)．
（1）求拋物線的函數(shù)表達(dá)式；
（2）點(diǎn)D在拋物線的對稱軸上，且位于x軸的上方，將△BCD沿直線BD翻折得到△BC'D，若點(diǎn)C'恰好落在拋物線的對稱軸上，求點(diǎn)C'和點(diǎn)D的坐標(biāo)；
（3）設(shè)P是拋物線上位于對稱軸右側(cè)的一點(diǎn)，點(diǎn)Q在拋物線的對稱軸上，當(dāng)△CPQ為等邊三角形時，求直線BP的函數(shù)表達(dá)式．組卷：6156引用：8難度：0.2 -
25．【問題提出】如圖1，在Rt△ABC中，∠ACB=90°，點(diǎn)E，F(xiàn)分別為邊AC，BC的中點(diǎn)，將△EFC繞點(diǎn)C順時針旋轉(zhuǎn)α（0°＜α＜360°），連接AE，BF，試探究AE，BF之間存在怎樣的數(shù)量關(guān)系和位置關(guān)系？
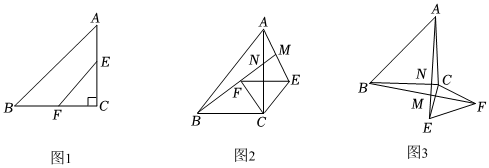
【特例探究】若AC=BC，將△EFC繞點(diǎn)C順時針旋轉(zhuǎn)至圖2的位置，直線BF與AE，AC分別交于點(diǎn)M，N．按以下思路完成填空（第一個空填推理依據(jù)，第二個空填數(shù)量關(guān)系，第三個空填位置關(guān)系）：
∵AC=BC，點(diǎn)E，F(xiàn)分別為邊AC，BC的中點(diǎn)，
∴CE=CF．
∵∠ACB=∠ECF，
∴∠ACE=∠BCF．
∴△ACE≌△BCF（ ）．
∴AE BF，∠CAE=∠CBF．
又∵∠ANM=∠BNC，
∴∠AMN=∠BCN=90°．
∴AE BM．
【猜想證明】若BC=nAC（n＞1），△EFC繞點(diǎn)C順時針旋轉(zhuǎn)至圖3的位置，直線AE與BF，BC分別交于點(diǎn)M，N，猜想AE與BF之間的數(shù)量關(guān)系與位置關(guān)系，并就圖3所示的情況加以證明；
【拓展運(yùn)用】若AC=4，BC=6，將△EFC繞點(diǎn)C順時針旋轉(zhuǎn)α（0°＜α＜360°），直線AE與BF相交于點(diǎn)M，當(dāng)以點(diǎn)C，E，M，F(xiàn)為頂點(diǎn)的四邊形是矩形時，請直接寫出BM的長．組卷：55引用：3難度：0.5