北師大新版八年級上冊《1.1 探索勾股定理》2021年同步練習卷(3)
發布:2024/4/20 14:35:0
一.選擇題(共5小題)
-
1.在△ABC中,∠C=90°,AC=8,BC=6,則AB的長為( )
A.5 B.10 C. 27D.28 組卷:990引用:8難度:0.9 -
2.直角三角形的兩直角邊的長分別為3,5,第三邊長為( )
A.4 B. 34C.4或 34D.4和 34組卷:65引用:4難度:0.9 -
3.在勾股定理的學習過程中,我們已經學會了運用如圖圖形,驗證著名的勾股定理,這種根據圖形直觀推論或驗證數學規律和公式的方法,簡稱為“無字證明”.實際上它也可用于驗證數與代數,圖形與幾何等領域中的許多數學公式和規律,它體現的數學思想是( )
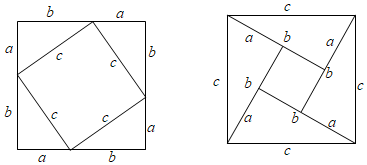
A.統計思想 B.分類思想 C.數形結合思想 D.函數思想 組卷:2656引用:43難度:0.8 -
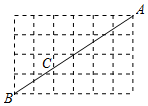 4.如圖,點A,B都在格點上,若BC=,則AC的長為( )2133
4.如圖,點A,B都在格點上,若BC=,則AC的長為( )2133A. 13B. 4133C. 213D. 313組卷:211引用:3難度:0.5 -
5.△ABC中,已知AB=1,AC=2.要使∠B是直角,BC的長度是( )
A. 3B. 5C.3 D. 或35組卷:596引用:6難度:0.8
三.解答題(共5小題)
-
14.已知直角三角形的兩直角邊長分別為(2+
)和(2-3).3
求這個直角三角形的斜邊長.組卷:317引用:3難度:0.8 -
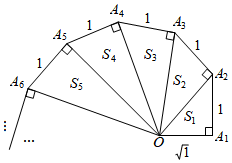 15.規律探索題:細心觀察如圖,認真分析各式,然后解答問題.;OA22=(1)2+1=2(S1是△OA1A2的面積);S1=12;OA32=(2)2+1=3(S2是△OA2A3的面積);S2=22;OA42=(3)2+1=4(S3是△OA3A4的面積);S3=32
15.規律探索題:細心觀察如圖,認真分析各式,然后解答問題.;OA22=(1)2+1=2(S1是△OA1A2的面積);S1=12;OA32=(2)2+1=3(S2是△OA2A3的面積);S2=22;OA42=(3)2+1=4(S3是△OA3A4的面積);S3=32
…
(1)請用含有n(n為正整數)的等式Sn=;
(2)推算出OA10=;
(3)求出的值.1S1+S2+1S2+S3+1S3+S4+1S4+S5組卷:1884引用:11難度:0.4


