2023年寧夏石嘴山三中高考數(shù)學(xué)四模試卷（理科）

一、選擇題：本題共12小題，每小題5分，共60分.在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的.

• 1．在復(fù)平面上，復(fù)數(shù)（-1+2i）²對(duì)應(yīng)的點(diǎn)在（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：41引用：4難度：0.8

  解析

• 2．已知全集U={x|x≥0}，集合A={x|x（x-2）≤0}，則?_UA=（　　）

  A．（2，+∞）	B．[2，+∞）
  C．（-∞，0）∪（2，+∞）	D．（-∞，0]∪[2，+∞）
  組卷：86引用：3難度：0.7

  解析

• 3．對(duì)于直線(xiàn)l和平面α，“直線(xiàn)l不在平面α上“是“l(fā)∥α“的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：58引用：4難度：0.7

  解析

• 4．我國(guó)是人口大國(guó)，21世紀(jì)以來(lái)的22年中（2001-2022年），人口出生數(shù)量（萬(wàn)）的變化趨勢(shì)如圖所示，則下列說(shuō)法錯(cuò)誤的是（　　）
  

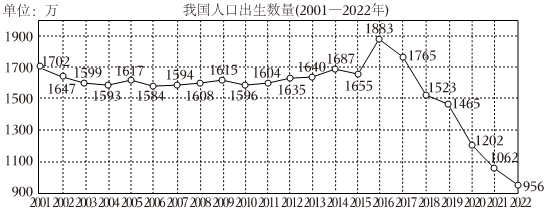
  A．22年中，人口出生數(shù)量的極差大于900萬(wàn)

  B．22年中，人口出生數(shù)量的中位數(shù)是1606萬(wàn)

  C．22年中，按平均數(shù)來(lái)考查，人口出生數(shù)量最近4年的平均數(shù)與最初4年的平均數(shù)之差的絕對(duì)值大于500萬(wàn)

  D．近6年，人口出生數(shù)量呈現(xiàn)逐年下降的趨勢(shì)
  組卷：15引用：2難度：0.7

  解析

• 5．將函數(shù)

  y

  =

  2

  co

  s

  2

  x

  2

  -

  1

  的圖象向右平移

  π

  4

  個(gè)單位長(zhǎng)度，所得圖象對(duì)應(yīng)的函數(shù)（　　）

  A．在區(qū)間 [ - π 6 ， π 3 ] 上單調(diào)遞增

  B．在區(qū)間 [ - π 6 ， π 3 ] 上單調(diào)遞減

  C．在區(qū)間 [ 5 π 12 ， 7 π 12 ] 上單調(diào)遞增

  D．在區(qū)間 [ 5 π 12 ， 7 π 12 ] 上單調(diào)遞減
  組卷：302引用：3難度：0.7

  解析

• 6．在遞增等比數(shù)列{a_n}中，其前n項(xiàng)和為S_n，且6a₇是a₈和a₉的等差中項(xiàng)，則

  S

  6

  S

  3

  =（　　）

  A．28

  B．20

  C．18

  D．12
  組卷：305引用：10難度：0.6

  解析

• 7．已知雙曲線(xiàn)C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的一條漸近線(xiàn)與直線(xiàn)2x-y+1=0垂直，則該雙曲線(xiàn)C的離心率為（　　）

  A． 5 2

  B． 3

  C．2

  D． 5
  組卷：185引用：2難度：0.7

  解析

（二）選考題：共10分．請(qǐng)考生在第22，23題中任選一題作答，如果多做，那么按所做的第一題計(jì)分．【選修4-4：坐標(biāo)系與參數(shù)方程】

• 22．在直角坐標(biāo)系xOy中，曲線(xiàn)C₁的參數(shù)方程為

  x = m + 1

  y = - 2 m

  （m為參數(shù)），以坐標(biāo)原點(diǎn)O為極點(diǎn)，x軸正半軸為極軸建立極坐標(biāo)系，曲線(xiàn)C₂的極坐標(biāo)方程為

  ρ

  =

  4

  cosθ

  si

  n

  2

  θ

  ．
  （1）求曲線(xiàn)C₁的普通方程與曲線(xiàn)C₂的直角坐標(biāo)方程；
  （2）已知點(diǎn)A（1，0），曲線(xiàn)C₁與曲線(xiàn)C₂交于E，F(xiàn)兩點(diǎn)，求

  1

  |

  AE

  |

  +

  1

  |

  AF

  |

  的值．
  組卷：8引用：2難度：0.6

  解析

【選修4-5：不等式選講】

• 23．已知函數(shù)f（x）=2|x|+|x-2|的最小值為m.
  （1）求m的值；
  （2）若實(shí)數(shù)a,b滿(mǎn)足a²+b²=m,求

  1

  1

  +

  a

  2

  +

  1

  2

  +

  b

  2

  的最小值．
  組卷：135引用：4難度：0.8

  解析