2022-2023學(xué)年江蘇省泰州二中附中九年級(jí)（上）期末數(shù)學(xué)試卷

一、選擇題（本大題共有6小題，每小題3分，共18分．在每小題所給出的四個(gè)選項(xiàng)中，恰有一項(xiàng)是符合題目要求的，請(qǐng)將正確選項(xiàng)的字母代號(hào)填涂在答題卡相應(yīng)位置上）

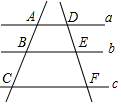• 1．如圖，直線a∥b∥c,直線AC分別交a,b,c于點(diǎn)A，B，C：直線DF分別交a,b,c于點(diǎn)D，E，F(xiàn)．若

  AB

  BC

  =

  2

  3

  ，則

  DE

  DF

  =（　　）

  A． 2 3

  B． 2 5

  C． 3 5

  D． 3 2
  組卷：793引用：4難度：0.6

  解析

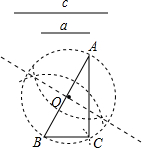• 2．數(shù)學(xué)課上，老師讓學(xué)生尺規(guī)作圖畫Rt△ABC，使其斜邊AB=c,一條直角邊BC=a.小明的作法如圖所示，你認(rèn)為這種作法中判斷∠ACB是直角的依據(jù)是（　　）

  A．勾股定理

  B．直徑所對(duì)的圓周角是直角

  C．勾股定理的逆定理

  D．90°的圓周角所對(duì)的弦是直徑
  組卷：1336引用：50難度：0.9

  解析

• 3．已知一個(gè)正多邊形的內(nèi)角是140°，則它是幾邊形（　　）

  A．10

  B．9

  C．8

  D．7
  組卷：421引用：7難度：0.6

  解析

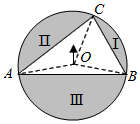• 4．如圖，轉(zhuǎn)盤中點(diǎn)A，B，C在圓上，∠A=40°，∠B=60°，讓轉(zhuǎn)盤繞圓心O自由轉(zhuǎn)動(dòng)，當(dāng)轉(zhuǎn)盤停止時(shí)指針指向區(qū)域Ⅲ的概率是（　　）

  A． 2 9

  B． 1 3

  C． 4 9

  D． 5 9
  組卷：239引用：2難度：0.7

  解析

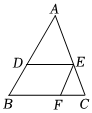• 5．如圖，在△ABC中，DE∥BC，EF∥AB，記S_△ADE=16，S_△EFC=4，則S_{平行四邊形DBFE}=（　　）

  A．9

  B．12

  C．16

  D．20
  組卷：610引用：3難度：0.6

  解析

• 6．在平面直角坐標(biāo)系中，設(shè)函數(shù)y=ax²+（a-1）x-1（a是常數(shù)，a≠0）
  ①若a＞0，則該函數(shù)圖象與x軸一定有兩個(gè)交點(diǎn)，而且在原點(diǎn)兩側(cè)．
  ②無(wú)論a取何值，該函數(shù)圖象必定經(jīng)過兩個(gè)定點(diǎn)．則（　　）

  A．①錯(cuò)誤，②錯(cuò)誤	B．①正確，②錯(cuò)誤
  C．①錯(cuò)誤，②正確	D．①正確，②正確
  組卷：452引用：2難度：0.6

  解析

二、填空題（本大題共有10小題，每小題3分，共30分，請(qǐng)把答案直接填寫在答題卡相應(yīng)位置上）

• 7．已知線段a=4，線段b=9，則a,b的比例中項(xiàng)是

  ．
  組卷：575引用：4難度：0.5

  解析

• 8．若⊙O的半徑為3cm,點(diǎn)A與圓心O的距離為4cm,則點(diǎn)A與⊙O的位置關(guān)系是

  ．
  組卷：410引用：5難度：0.7

  解析

三、解答題（本大題共有10題，共102分，請(qǐng)?jiān)诖痤}卡規(guī)定區(qū)域內(nèi)作答，解答時(shí)應(yīng)寫出必要的文字說明、證明過程或演算步驟）

• 25．（1）如圖1，D、E為等邊△ABC中BC邊所在直線上兩點(diǎn)，∠DAE=120°，求證：△ABD∽△ECA；
  （2）△ADE中，∠DAE=120°，請(qǐng)用不含刻度的直尺和圓規(guī)在DE上求作兩點(diǎn)B、C，點(diǎn)B在點(diǎn)C的左側(cè)，使得△ABC為等邊三角形；
  （3）在（1）的條件下，H為BC邊上一點(diǎn)，過H作HF∥AD交AB延長(zhǎng)線于點(diǎn)F，HG∥AE交AC延長(zhǎng)線于點(diǎn)G，若AB=6，BD=a,∠HAE=60°，求

  HF

  HG

  的值．（用含有a的代數(shù)式表示）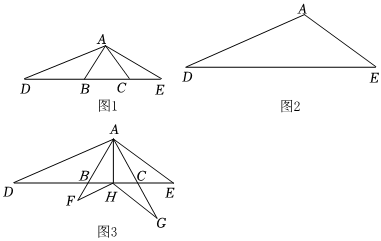
  組卷：360引用：2難度：0.1

  解析

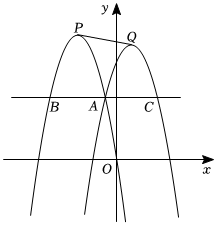• 26．在平面直角坐標(biāo)系中，已知拋物線

  y

  1

  =

  -

  x

  2

  -

  6

  x

  ．
  （1）求拋物線y₁的頂點(diǎn)P坐標(biāo)；
  （2）平移拋物線y₁得拋物線y₂，兩拋物線交于點(diǎn)A，過點(diǎn)A作x軸的平行線交拋物線y₁和平移后的拋物線y₂分別為B和C（點(diǎn)B在點(diǎn)C的左側(cè)）．
  ①平移后的拋物線y₂頂點(diǎn)在直線x=1上，點(diǎn)A的橫坐標(biāo)為-1，求拋物線y₂的表達(dá)式；
  ②平移后的拋物線y₂頂點(diǎn)在直線x=1上，點(diǎn)A的橫坐標(biāo)為m（-3＜m＜1），求BC的長(zhǎng)；
  ③設(shè)點(diǎn)A的橫坐標(biāo)為n,BC=10，拋物線y₂的頂點(diǎn)為Q，設(shè)PQ²=y,求y關(guān)于n的函數(shù)表達(dá)式，并求PQ的最小值．
  組卷：449引用：2難度：0.4

  解析