2023-2024學年貴州省遵義市紅花崗區四校聯考九年級（上）期中數學試卷

一、選擇題（以下每題均有A、B、C、D四個選項，其中只有一個選項正確。每題3分，共36分）.

• 1．下列航天圖標中，其圖案是中心對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：121引用：9難度：0.9

  解析

• 2．在平面直角坐標系xOy中，點A（-1，2）關于原點對稱的點的坐標是（　　）

  A．（1，-2）

  B．（-1，2）

  C．（-2，1）

  D．（-1，-2）
  組卷：824引用：11難度：0.9

  解析

• 3．若x=2是關于x的一元二次方程x²-mx+5=0的一個根，則m的值是（　　）

  A．2

  B．-2

  C． 9 2

  D． - 9 2
  組卷：227引用：3難度：0.5

  解析

• 4．把拋物線y=x²+1向右平移3個單位，再向下平移2個單位，得到拋物線（　　）

  A．y=（x+3）2-1

  B．y=（x+3）2+3

  C．y=（x-1）2-1

  D．y=（x-3）2-1
  組卷：157引用：10難度：0.9

  解析

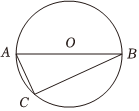• 5．如圖，AB是⊙O的直徑，∠B=30°，AC=1，則AB的長為（　　）

  A． 3

  B．2

  C． 2 3

  D．3
  組卷：99引用：1難度：0.7

  解析

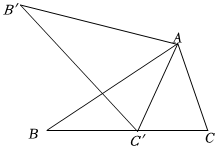• 6．如圖，在△ABC中，∠C=65°，將△ABC繞著點A順時針旋轉后，得到△AB′C′，且點C′在BC上，則∠B′C′B的度數為（　　）

  A．54°

  B．45°

  C．46°

  D．50°
  組卷：264引用：3難度：0.5

  解析

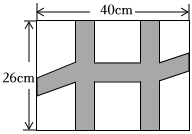• 7．現要在一個長為40m,寬為26m的矩形花園中修建等寬的小道，剩余的地方種植花草．如圖所示，要使種植花草的面積為864m²，若設小道的寬度為x m,則由題意可列方程為（　　）

  A．（40-2x）（26-x）=40×26-864

  B．（40-2x）（26-x）=864

  C．（40-x）（26-2x）=864

  D．（40-2x）（26-x）+2x2=864
  組卷：111引用：5難度：0.7

  解析

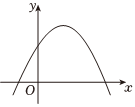• 8．在平面直角坐標系中，二次函數y=ax²+bx+c的圖象如圖所示，則點P（ac,b）所在象限是（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：175引用：4難度：0.8

  解析

三、解答題（本大題共9題，共計98分，解答應寫出必要的文字說明、證明過程或演算步驟）.

• 24．在2024年元旦即將到來之際，學校準備開展“冬日情暖，喜迎元旦”活動，小星同學對會場進行裝飾．如圖1所示，他在會場的兩墻AB、CD之間懸掛一條近似拋物線y=ax²-

  4

  5

  x+3的彩帶，如圖2所示，已知墻AB與CD等高，且AB、CD之間的水平距離BD為8米．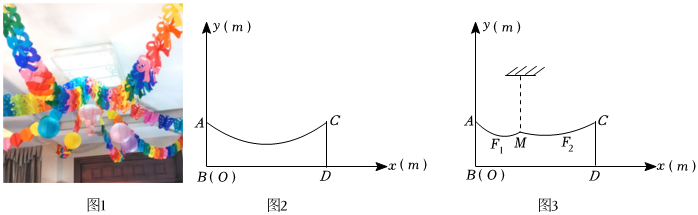
  
  （1）如圖2，兩墻AB，CD的高度是

  米，拋物線的頂點坐標為

  ；
  （2）為了使彩帶的造型美觀，小星把彩帶從點M處用一根細線吊在天花板上，如圖3所示，使得點M到墻AB距離為3米，使拋物線F₁的最低點距墻AB的距離為2米，離地面2米，求點M到地面的距離；
  （3）為了盡量避免人的頭部接觸到彩帶，小星現將M到地面的距離提升為3米，通過適當調整M的位置，使拋物線F₂對應的二次函數的二次項系數始終為

  1

  5

  ，若設點M距墻AB的距離為m米，拋物線F₂的最低點到地面的距離為n米，探究n與m的關系式，當

  2

  ≤

  n

  ≤

  9

  4

  時，求m的取值范圍．
  組卷：939引用：9難度：0.3

  解析

• 25．如圖1，已知△ABC，AC=BC，∠ACB=90°，點D平面內的一點，連接CD，將線段CD繞點C順時針方向旋轉90°得到CE，連接BD，AE．
  （1）【問題發現】
  如圖1，若點D為△ABC內的一點，線段BD與AE的數量關系是

  ，線段BD與AE位置關系是

  ；
  （2）【問題探究】
  如圖2，若點D為△ABC外的一點，連接BE，若AB=BE，探究線段AD與CD的數量關系，并說明理由；
  （3）【拓展延伸】
  如圖3，若點D為△ABC外的一點，且BC=2，

  CD

  =

  2

  2

  ．∠ACD=α（0＜α＜180°），當△BDE是以BE為腰的等腰三角形時，求BD²的值．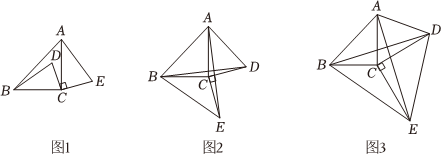
  ?
  組卷：157引用：1難度：0.1

  解析