2023年湖南省長沙市開福區立信中學中考數學三模試卷

一、選擇題（本大題共10個小題，每小題3分，共30分）

• 1．下列各數中，無理數的是（　　）

  A． 11 7

  B． 4

  C． 3 8

  D．π
  組卷：43引用：1難度：0.7

  解析

• 2．最近，武漢一教師憑借“挖呀挖呀挖…”的視頻火遍全網，新華網以《幼兒園老師用溫暖的歌曲，帶給花朵們溫馨的童年》為題，轉發了這則視頻，短時間內點贊突破435萬，435萬用科學記數法表示為（　　）

  A．4.35×102

  B．43.5×105

  C．4.35×106

  D．0.435×107
  組卷：111引用：2難度：0.8

  解析

• 3．甲骨文是我國的一種古代文字，是漢字的早期形式，下列甲骨文中，不是軸對稱的是（　　）

  A．

  B．

  C．

  D．
  組卷：174引用：8難度：0.6

  解析

• 4．下列運算正確的是（　　）

  A．（a2）3=a5	B．（a+2）2=a2+4
  C． 24 ÷ 6 = 2	D．-3（a-2b）=-3b+2b
  組卷：62引用：3難度：0.8

  解析

• 5．如果一個多邊形的內角和等于900°，這個多邊形是（　　）

  A．四邊形

  B．五邊形

  C．六邊形

  D．七邊形
  組卷：970引用：21難度：0.9

  解析

• 6．下列說法正確的是（　　）

  A．了解一批燈泡的使用壽命，應采用全面調查

  B．圓的切線垂直于圓的半徑

  C．角平分線上任意一點到角兩邊的距離相等

  D．“明天降雨概率90%”，指明天有90%的時間在下雨
  組卷：52引用：1難度：0.6

  解析

• 7．如圖，△ABC是等邊三角形，邊長為2，根據作圖的痕跡，則BD的長為（　　）

  A．1.7

  B． 3

  C． 5

  D． 6
  組卷：188引用：8難度：0.7

  解析

• 8．搶微信紅包成為節日期間人們最喜歡的活動之一．對某單位50名員工在春節期間所搶的紅包金額進行統計，并繪制成了如下統計圖．根據如圖提供的信息，紅包金額的眾數和中位數分別是（　　）

  A．30，30

  B．30，20

  C．40，40

  D．30，40
  組卷：416引用：10難度：0.7

  解析

三、解答題（共9個小題，第17、18、19題每題6分，第20、21題每題8分，第22、23題每題9分，第24、25題每題10分，共72分。解答應寫出必要的文字說明、證明過程或演算步驟）

• 24．我們定義：若點P在一次函數y=ax+b（a≠0）圖象上，點Q在反比例函數

  y

  =

  c

  x

  （c≠0）圖象上，且滿足點P與點Q關于y軸對稱，則稱二次函數y=ax²+bx+c為一次函數y=ax+b與反比例函數

  y

  =

  c

  x

  的“衍生函數”，點P稱為“基點”，點Q稱為“靶點”．
  （1）若二次函數y=x²+2x+1是一次函數y=ax+b與反比例函數

  y

  =

  c

  x

  的“衍生函數”，則a=

  ，b=

  ，c=

  ；
  （2）若一次函數y=x+b和反比例函數

  y

  =

  c

  x

  的“衍生函數”的頂點在x軸上，且“基點”P的橫坐標為1，求“靶點”的坐標；
  （3）若一次函數y=ax+2b（a＞b＞0）和反比例函數

  y

  =

  -

  2

  x

  的“衍生函數”經過點（2，6）．①試說明一次函數y=ax+2b圖象上存在兩個不同的“基點”；②設一次函數y=ax+2b圖象上兩個不同的“基點”的橫坐標為x₁、x₂，求|x₁-x₂|的取值范圍．
  組卷：825引用：3難度：0.3

  解析

• 25．如圖1，直線l：y=-

  3

  4

  x+b與x軸交于點A（4，0），與y軸交于點B，點C是線段OA上一動點（0＜AC＜

  16

  5

  ）．以點A為圓心，AC長為半徑作⊙A交x軸于另一點D，交線段AB于點E，連接OE并延長交⊙A于點F．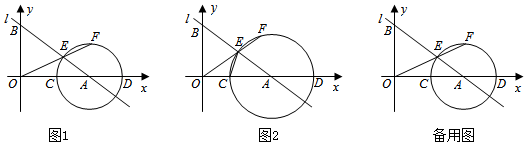
  
  （1）求直線l的函數表達式和tan∠BAO的值；
  （2）如圖2，連接CE，當CE=EF時，
  ①求證：△OCE∽△OEA；
  ②求點E的坐標；
  （3）當點C在線段OA上運動時，求OE?EF的最大值．
  組卷：5296引用：10難度：0.1

  解析