2021-2022學(xué)年湖南省岳陽市開發(fā)區(qū)長嶺中學(xué)七年級(jí)（下）期中數(shù)學(xué)試卷

一、選擇題：（每小題3分，共24分．在每道小題給出的四個(gè)選項(xiàng)中，選出符合要求的一項(xiàng)．）

• 1．下列方程組中是二元一次方程組的是（　　）

  A． xy = 1 x + y = 2	B． 5 x - 2 y = 3 1 x + y = 3
  C． 2 x + z = 0 3 x - y = 5	D． x = 1 2 x + 3 y = 5
  組卷：53引用：2難度：0.7

  解析

• 2．下列運(yùn)算正確的是（　　）

  A．x?x4=x5

  B．（a2）3=a5

  C．3x2-x2=3

  D．（2x2）3=6x6
  組卷：23引用：4難度：0.7

  解析

• 3．下列等式從左到右的變形中，屬于因式分解的是（　　）

  A．6a2b3=2ab?3ab2

  B．x2-6x=x（x-6）

  C．（x+2）2=x2+4x+4

  D．x2-4+4x=（x+2）（x-2）+4x
  組卷：9引用：3難度：0.8

  解析

• 4．方程組

  ax - by = 1

  ax + by = 7

  的解是

  x = 2

  y = 1

  ，則a,b的值為（　　）

  A． a = 3 b = 2

  B． a = 2 b = 3

  C． a = 3 b = 1

  D． a = 2 b = 1
  組卷：14引用：2難度：0.7

  解析

• 5．已知a²+2a-2=0，則2a²+4a+3的值為（　　）

  A．1

  B．5

  C．6

  D．7
  組卷：33引用：3難度：0.7

  解析

• 6．岳陽市第十九中學(xué)七年級(jí)某班進(jìn)行體育訓(xùn)練，若每組7人，余3人；若每組8人，則缺5人．設(shè)組數(shù)為x組，總?cè)藬?shù)為y人，則可列方程組為（　　）

  A． 7 x + 3 = y 8 x - 5 = y	B． 7 y = x + 3 8 y - 5 = x
  C． 7 y = x - 3 8 y + 5 = x	D． 7 y = x - 3 8 y = x + 5
  組卷：20引用：4難度：0.7

  解析

• 7．對(duì)于任意的有理數(shù)a,b,c,d,我們規(guī)定

  a	b
  c	d

  =ad-bc,如

  1	2
  3	4

  =1×4-2×3=-2．求

  （ a + c ）	（ b - a ） 2
  （ a - c ）	（ a - b ） 2

  的值為（　　）

  A．2c（a-b）2

  B．2a（a-b）2

  C．（a-c）（a-b）

  D．（a-c）（a+c）
  組卷：24引用：2難度：0.7

  解析

• 8．已知：a=81⁴，b=27⁵，c=9⁷，則a,b,c的大小關(guān)系是（　　）

  A．a(chǎn)＞b＞c

  B．a(chǎn)＞c＞b

  C．a(chǎn)＜b＜c

  D．b＞c＞a
  組卷：154引用：6難度：0.9

  解析

三、解答題：（本大題共8小題，共64分．解答應(yīng)寫出文字說明、解題過程或演算步驟．）

• 23．閱讀題目并回答下列問題：
  （1）為了求整式x²+2x+3的值，我們必須知道x的值．
  若x=1，則x²+2x+3的值為

  ；
  若x=2，則x²+2x+3的值為

  ．
  可見，這個(gè)整式的值因x的取值不同而變化，盡管如此，我們還是沒有辦法來考慮這個(gè)整式的值的范圍；
  （2）若把一個(gè)多項(xiàng)式進(jìn)行部分因式分解可以來解決整式值的最大（或最小）值問題．例如：x²+2x+3=（x²+2x+1）+2=（x+1）²+2．因?yàn)椋▁+1）²是非負(fù)數(shù)，所以x²+2x+3的最小值是

  ，這時(shí)相應(yīng)的x的值是

  ；
  （3）嘗試探究并解答：
  ①求x²-10x+35的最小值，并寫出相應(yīng)x的值；
  ②求-x²-8x+15的最大值，并寫出相應(yīng)的x的值．
  組卷：49引用：2難度：0.5

  解析

• 24．數(shù)學(xué)活動(dòng)課上，老師準(zhǔn)備了圖1中三種不同大小的正方形與長方形，拼成了一個(gè)如圖2所示的正方形．
  
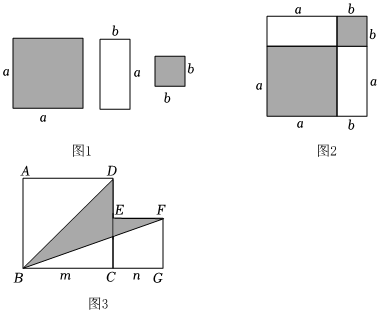
  （1）請(qǐng)用兩種不同的方法表示圖2中陰影部分的面積和．
  方法1：

  ；方法2：

  ．
  （2）請(qǐng)你直接寫出三個(gè)代數(shù)式：（a+b）²，a²+b²，ab之間的等量關(guān)系．
  （3）利用（2）中結(jié)論解決下面的問題：
  ①如圖3，兩個(gè)正方形邊長分別為m,n,如果m+n=4，mn=1，求陰影部分的面積．
  ②已知（x-2021）²+（2023-x）²=10，求（x-2021）（2023-x）的值．
  組卷：79引用：2難度：0.7

  解析