2022-2023學年陜西省西安三中高二（下）第二次測評數學試卷（理科）
發(fā)布：2024/6/29 8:0:10
一、選擇題（本題共12小題，每小題5分，共60分）
-
1．已知集合A={y|y=2x-1}，B={x|y=log0.5（2-x）}，則A∩B=（ ）
組卷：160引用：3難度：0.7 -
2．設x∈R，向量
，a=（1，2），b=（x,1）．則“c=（4，x）”是“a⊥b”的（ ）b∥c組卷：139引用：6難度：0.7 -
3．已知命題p：?x≥0，x2-x≥0，則￢p為（ ）
組卷：105引用：3難度：0.8 -
4．隨機變量X的分布列如下，則D（X）的最大值是（ ）
X 0 1 P a b 組卷：32引用：1難度：0.5 -
5．設命題p：方程
表示焦點在y軸上的橢圓；命題q：方程x2k+1+y23-k=1表示焦點在x軸上的雙曲線，若p∧q為真，則實數k的取值范圍（ ）x2k+1+y2k-2=1組卷：16引用：5難度：0.8 -
6．某射手每次射擊擊中目標的概率均為P（0＜P＜1），且各次射擊的結果互不影響．設隨機變量X為該射手在n次射擊中擊中目標的次數，若
，則P的值為（ ）E（X）=4，D（X）=43組卷：53引用：3難度：0.7 -
7．已知a=
2π∫20dx,若（1-ax）2018=b0+b1x+b2x2+…+b2018x2018（x∈R），則4-x2b12+b222的值為（ ）+…+b201822018組卷：138引用：2難度：0.6
三、解答題（本題共6小題，共70分）
-
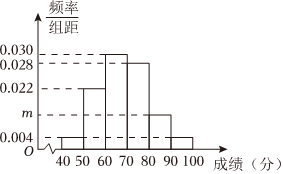21．地區(qū)期末進行了統(tǒng)一考試，為做好本次考試的評價工作，將本次成績轉化為百分制，現從中隨機抽取了50名學生的成績，經統(tǒng)計，這批學生的成績全部介于40至100之間，將數據按照[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]分成6組，制成了如圖所示的頻率分布直方圖．
（1）求頻率分布直方圖中m的值；
（2）在這50名學生中用分層抽樣的方法從成績在[70，80），[80，90），[90，100]的三組中抽取了11人，再從這11人中隨機抽取3人，記ξ為3人中成績在[80，90）的人數，求ξ的分布列和數學期望；
（3）轉化為百分制后，規(guī)定成績在[90，100]的為A等級，成績在[70，90）的為B等級，其它為C等級．以樣本估計總體，用頻率代替概率．從所有參加考試的同學中隨機抽取3人，求獲得B等級的人數不少于2人的概率．組卷：252引用：4難度：0.6 -
22．在某公司舉行的一次真假游戲的有獎競猜中，設置了“科技”和“生活”這兩類試題，規(guī)定每位職工最多競猜3次，每次競猜的結果相互獨立．猜中一道“科技”類試題得4分，猜中一道“生活”類試題得2分，兩類試題猜不中的都得0分．將職工得分逐次累加并用X表示，如果X的值不低于4分就認為通過游戲的競猜，立即停止競猜，否則繼續(xù)競猜，直到競猜完3次為止．競猜的方案有以下兩種：方案1：先猜一道“科技”類試題，然后再連猜兩道“生活”類試題；
方案2：連猜三道“生活”類試題．
設職工甲猜中一道“科技”類試題的概率為0.5，猜中一道“生活”類試題的概率為0.6．
（1）你認為職工甲選擇哪種方案通過競猜的可能性大？并說明理由．
（2）職工甲選擇哪一種方案所得平均分高？并說明理由．組卷：154引用：3難度：0.5